Analytical Elastostatic Contact Mechanics of Highly-Loaded Contacts of Varying Conformity
Abstract
:1. Introduction
2. Determination of 2D Sub-Surface Stress Field
2.1. Case of Non-Conforming Semi-Infinite Solids
2.2. Case of Conforming Elastic Solids
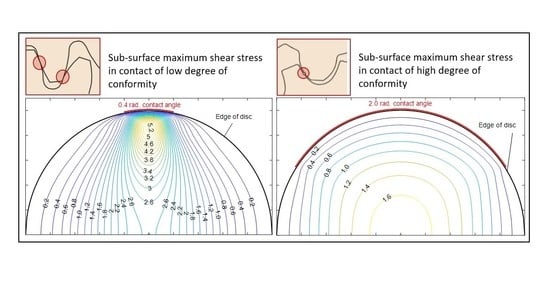
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman Symbols | |
| Hertzian semi-minor half-width | |
| b | Hertzian semi-major half-width |
| D | Diameter of the disc |
| E | Modulus of elasticity |
| p | Pressure |
| Maximum pressure | |
| Radii of contacting bodies at the point of contact | |
| W | Applied line load |
| Location in the depth of a contacting solid | |
| Location measured from an applied line load | |
| Location of a pressure element, p | |
| Greek Symbols | |
| Arc location of a pressure element, p | |
| Half arc extent of a curvilinear contact | |
| Radius difference of contacting pairs | |
| Poisson’s ratio | |
| Direct sub-surface stresses | |
| Orthogonal sub-surface shear stress | |
| Maximum sub-surface shear stress | |
References
- Evans, H.P.; Snidle, R.W. Wildhaber-Novikov circular arc gears: Elastohydrodynamics. J. Tribol. 1993, 115, 487–492. [Google Scholar] [CrossRef]
- Novikov, A.; Golovanov, V.; Dorofeyev, D.; Dorofeyev, V. Terminology and Design of Asymmetrical Gears for Aircraft. In Theory and Practice of Gearing and Transmissions; Springer: Cham, Switzerland, 2016; pp. 381–392. [Google Scholar]
- French, M.J. Conformity of circular-arc gears. J. Mech. Eng. Sci. 1965, 7, 220–223. [Google Scholar] [CrossRef]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology, 2nd ed.; Imperial College Press: London, UK, 2012. [Google Scholar]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Karagiannis, I.; Theodossiades, S.; Rahnejat, H. On the dynamics of lubricated hypoid gears. Mech. Mach. Theory 2012, 48, 94–120. [Google Scholar] [CrossRef] [Green Version]
- Kolivand, M.; Kahraman, A. An ease-off based method for loaded tooth contact analysis of hypoid gears having local and global surface deviations. J. Mech. Des. 2010, 132, 071004. [Google Scholar] [CrossRef]
- Elisaus, V.; Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Effect of teeth micro-geometrical form modification on contact kinematics and efficiency of high performance transmissions. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2017, 231, 538–555. [Google Scholar] [CrossRef] [Green Version]
- Fajdiga, G.; Glodež, S.; Kramar, J. Pitting formation due to surface and subsurface initiated fatigue crack growth in contacting mechanical elements. Wear 2007, 262, 1217–1724. [Google Scholar] [CrossRef]
- Zhu, D.; Ren, N.; Wang, Q.J. Pitting life prediction based on a 3D line contact mixed EHL analysis and subsurface von Mises stress calculation. J. Tribol. 2009, 131, 041501. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. On the prediction of fatigue crack initiation in rolling/sliding contacts with provision for loading sequence effect. Tribol. Int. 2011, 44, 1620–1628. [Google Scholar] [CrossRef]
- Ioannides, E.; Harris, T.A. A new fatigue life model for rolling bearings. J. Tribol. 1985, 107, 367–377. [Google Scholar] [CrossRef]
- Huber, M.T. Zur Theorie der beruhrung fester elastischer korper. Ann. Phys. 1904, 319, 153–163. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.T.; Fuchs, S. Spannungverleitung bei der beruhrung zweier elastischer zylinder. Phys. Zeitschr. 1914, 15, 298–303. [Google Scholar]
- Lyman, J. Reversing normal strains produced by rolling contact load. J. Lubr. Technol. 1967, 89, 76–80. [Google Scholar] [CrossRef]
- Poritsky, H. Stresses and deflections of cylindrical bodies in contact with application to contact of gears and locomotive wheels. J. Appl. Mech. 1950, 18, 191–201. [Google Scholar]
- Johnson, K.L. One hundred years of Hertz contact. Proc. Inst. Mech. Eng. 1982, 196, 363–378. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Mihailidis, A.; Bakolas, V.; Drivakos, N. Subsurface stress field of a dry line contact. Wear 2001, 249, 546–556. [Google Scholar] [CrossRef]
- Sadeghi, F. Elastohydrodynamic lubrication. In Tribology and Dynamics of Engine and Powertrain; Rahnejat, H., Ed.; Woodhead Publishing: Cambridge/Shaston, UK, 2010; pp. 171–226. [Google Scholar]
- Rahnejat, H.; Rahmani, R.; Mohammadpour, M.; Johns-Rahnejat, P.M. Tribology of power train systems. In ASM Handbook, Vol. 18, Friction, Lubrication, and Wear Technology; Totten, G.E., Ed.; ASM International: Cleveland, OH, USA, 2017; pp. 916–934. [Google Scholar]
- Chidlow, S.J.; Teodorescu, M.; Vaughan, N.D. A solution method for the sub-surface stresses and local deflection of a semi-infinite inhomogeneous elastic medium. Appl. Math. Model. 2012, 36, 3486–3501. [Google Scholar] [CrossRef]
- Barber, J.R. Contact problems for the thin elastic layer. Int. J. Mech. Sci. 1990, 32, 129–132. [Google Scholar] [CrossRef] [Green Version]
- Teodorescu, M.; Rahnejat, H.; Gohar, R.; Dowson, D. Harmonic decomposition analysis of contact mechanics of bonded layered elastic solids. Appl. Math. Model. 2009, 33, 467–485. [Google Scholar] [CrossRef]
- Elsharkawy, A.A.; Hamrock, B.J. Subsurface stresses in micro-EHL line contacts. J. Tribol. 1991, 113, 645–655. [Google Scholar] [CrossRef]
- Zhu, D.; Hu, Y.Z. A computer program package for the prediction of EHL and mixed lubrication characteristics, friction, subsurface stresses and flash temperatures based on measured 3-D surface roughness. Tribol. Trans. 2001, 44, 383–390. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Gao, P. A study of spur gear pitting under EHL conditions: Theoretical analysis and experiments. Tribol. Int. 2016, 94, 146–154. [Google Scholar] [CrossRef]
- Sivayogan, G.; Rahmani, R.; Rahnejat, H. Lubricated loaded tooth contact analysis and non-newtonian thermoelastohydrodynamics of high-performance spur gear transmission systems. Lubricants 2020, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Johns-Rahnejat, P.M.; Gohar, R. Point contact elastohydrodynamic pressure distribution and sub-surface stress field. In Proceedings of the Tri-Annual Conference on Multi-Body Dynamics: Monitoring and Simulation Techniques, Bradford, UK, 21 March 1997. [Google Scholar]
- Czyzewski, T. Changes in the stress field in the elastohydrodynamic contact zone in the rolling contact fatigue of cylindrical surfaces. Wear 1975, 31, 119–140. [Google Scholar] [CrossRef]
- Sackfield, A.; Hills, D.A. Some useful results in the classical Hertzian contact problem. J. Strain Anal. Eng. Des. 1983, 18, 101–105. [Google Scholar] [CrossRef]
- Sackfield, A.; Hills, D.A. Some useful results in the tangentially loaded Hertzian contact problem. J. Strain Anal. Eng. Des. 1983, 18, 107–110. [Google Scholar] [CrossRef]
- Love, A.E.H. The stress produced in a semi-infinite solid by pressure on part of the boundary. Phil. Trans. Roy. Soc. Lond. A 1929, 228, 377–420. [Google Scholar]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff: Groningen, The Netherlands, 1963; p. 17404. [Google Scholar]
- Mohammadpour, M.; Johns-Rahnejat, P.M.; Rahnejat, H.; Gohar, R. Boundary conditions for elastohydrodynamics of circular point contacts. Tribol. Lett. 2013, 53, 107–118. [Google Scholar] [CrossRef] [Green Version]
- Gohar, R.; Safa, M.M. Measurement of contact pressure under elastohydrodynamic lubrication conditions. In Tribology and Dynamics of Engine and Powertrain; Woodhead Publishing: Cambridge/Shaston, UK, 2010; pp. 222–245. [Google Scholar]
- Bogdanski, S. A rolling contact fatigue crack driven by squeeze fluid film. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 1061–1071. [Google Scholar] [CrossRef]
- Hu, J.; Gao, F.; Liu, X.; Wie, Y. An elasto-plastic contact model for conformal contacts between cylinders. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019. [Google Scholar] [CrossRef] [Green Version]
- Kogut, L.; Etsion, K. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef] [Green Version]
- Kogut, L.; Etsion, I. Adhesion in elastic-plastic spherical microcontact. J. Colloid Interface Sci. 2003, 261, 372–378. [Google Scholar] [PubMed]
- Chong, W.W.F.; Teodorescu, M.; Rahnejat, H. Nanoscale elastoplastic adhesion of wet asperities. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 996–1010. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Analytical Elastostatic Contact Mechanics of Highly-Loaded Contacts of Varying Conformity. Lubricants 2020, 8, 89. https://doi.org/10.3390/lubricants8090089
Johns-Rahnejat PM, Dolatabadi N, Rahnejat H. Analytical Elastostatic Contact Mechanics of Highly-Loaded Contacts of Varying Conformity. Lubricants. 2020; 8(9):89. https://doi.org/10.3390/lubricants8090089
Chicago/Turabian StyleJohns-Rahnejat, Patricia M., Nader Dolatabadi, and Homer Rahnejat. 2020. "Analytical Elastostatic Contact Mechanics of Highly-Loaded Contacts of Varying Conformity" Lubricants 8, no. 9: 89. https://doi.org/10.3390/lubricants8090089
APA StyleJohns-Rahnejat, P. M., Dolatabadi, N., & Rahnejat, H. (2020). Analytical Elastostatic Contact Mechanics of Highly-Loaded Contacts of Varying Conformity. Lubricants, 8(9), 89. https://doi.org/10.3390/lubricants8090089