Investigation on Load Path of a Latticed Shell Structure under Localized Fire Based on Member Sensitivity

Abstract

Thermal expansion of a member can affect structural bearing capacity when one or more members are subjected to fire. To explore the developmental rule of member internal force in latticed shell structure, a computation method of member sensitivity is presented based on the alternate path method. Taking a K8 single-layer latticed shell structure as the analysis object, finite element models are established by ANSYS, applying temperature loads on radial and circumferent ribs, calculating the sensitivity of each member during heating, and exploring the rule of member sensitivity at different temperatures. It is revealed from the numerical results that when one member is in fire, member sensitivity is proportional to temperature and inversely proportional to the distance from the member subjected to fire. Taking the member sensitivity coefficient as an index, the internal force will be transmitted along the member with high sensitivity, the rule of load path and internal force redistribution is given when the latticed shell structure is under elevated temperature.

1. Introduction

Due to its lightweight, good rigidity, and large span, a spatial structure is mostly used in public buildings, such as stadiums and exhibition halls. Steel is the main material in a spatial structure, which has poor fire resistance; the material’s mechanical properties decrease as the temperature rises. Most members of the large-span space structure are axially compressed, and structural members are more likely to be damaged when the structure is in a fire. As one of the main secondary disasters of a building fire, progressive collapse is generally difficult to predict.

Progressive collapse of a building structure is defined as a local failure and unbalanced force caused by unexpected loads; it can cause member failure because internal force changes dramatically. Building fire is one of the disasters with high frequency and serious harm; it is also an occasional effect that seriously endangers the safety of spatial structures. Many scholars have carried out a series of studies on the progressive collapse resistance of building structures [1,2,3,4,5,6], especially for the mechanical response of large-span space structures subjected to fire; a number of conclusions have been obtained through fire experiments and FE analysis. Guo [7,8] carried out eight destructive fire tests on a scale-reticulated shell model. The experimental results show the shell specimen performed arching under vertical load and the fire effect due to thermal expansion, the global deformation patterns and the axial force distributions of the specimen were approximately symmetric when the fire was located at the center of the test model, and the ultimate bearing capacity of the specimen gradually decreased with the combustion of the fire. Yu [9] uses fire dynamics software FDS to set different fire source positions to generate the fire temperature field of the single-layer cylindrical reticulated shell and used the finite element software ABAQUS to conduct a numerical simulation of the behavior of the cylindrical shell structure under different fire conditions. The influence of several parameters, such as the steel pipe section size, rise span ratio of the structure, roof load, and thickness of the fireproof coating, on the single-layer cylindrical reticulated shell in fire is analyzed.

Sensitivity analysis is an analytical method to evaluate the parameter change of structural response while the structure is in particular load conditions; sensitivity index is commonly used in the analysis of the progressive collapse-resisting performance of building structures. Based on member sensitivity, many scholars have established a method to evaluate the progressive collapse-resisting performance of structures, such as the member importance index [10,11], structural redundancy index [12,13], and robustness analysis [14,15,16]. The load path analysis is an important problem of structural resistance to progressive collapse. Wang [17] investigates a test of a scaled Kiewitt-6 dome; the effects of force transmission paths and initial imperfections on the progressive collapse resistance of large-span single-layer latticed domes were analyzed. The results indicate that the failure mode of the tested dome was local collapse when the two force transmission paths failed. The dome relies mainly on the compression mechanism to resist progressive collapse. Zhao [18] proposes a new expression of internal stiffness to visualize the load paths, instead of measuring strain energy caused by displacement at the loading point. An L-bracket test is carried out to validate the index. However, these indexes are not applicable to the structure in fire because material properties attenuation at elevated temperature is not considered.

In the condition of a building fire, steel members are prone to fail, but it is a dynamic process of member failure as the temperature increases. The failure of a single member can cause damage to multiple adjacent members in the local zone; it is a great danger to structural safety. In order to clarify the internal forces redistribution rule and prevent progressive collapse when a single-layer latticed shell structure is subjected to fire, this study proposes a member sensitivity index considering material properties reduction, quantitative analyses of the member sensitivity at different temperatures through finite element analysis; the transmission path is determined through the member sensitivity change with temperature. The current work aims to evaluate the structure’s progressive collapse-resisting performance when a latticed shell structure is under fire conditions.

2. Member Sensitivity Index

Fire can cause serious adverse effects on the structure. The temperature of a building fire generally is greater than 800 °C. However, the mechanical properties of steel significantly decline at 500 °C. With the temperature rising, the thermal effect on the structure becomes more significant. This may cause two security concerns. On the one hand, the elevated temperature will reduce the member bearing capacity, which is easy to cause local failure; on the other hand, mutual support exists between members in a spatial structure, so the failure of local members may cause the progressive collapse of the structure. Therefore, in the process of heating up, exploring member sensitivity to temperature, and clarifying the force transmission path, ensure not only the fire resistance design safety of the structure but also provide a basis for the fire occurrence performance evaluation.

The sensitivity coefficient is an index used to quantitatively evaluate the vulnerability of a certain member; it reflects which member is more likely to fail than others under a specific working condition. The sensitivity coefficient of member SI is generally defined as Equation (1) [19].

$$\mathrm{SI}=\frac{\lambda -{\lambda }_0}{{\lambda }_0}$$

(1)

where ${\lambda }_0$ and $\lambda$ are the mechanical parameters of the initial state and the final state of the structure, respectively.

Equation (1) is suitable for structure sensitivity analysis at room temperature. However, steel is a thermosensitive material, and its mechanical properties change significantly with temperature. The elastic modulus and yield strength should be considered for materials at elevated temperatures, as temperatures can significantly affect the member sensitivity. When the structure is in fire, the fire-retardant coating of some members is burnt out; these members are directly exposed to fire and rapidly heat up; in contrast, other members heat slowly because of the protection of the fire-retardant coating. There is a temperature difference and stress difference between the two types, resulting in an uneven temperature distribution of the members in the structure. To quantitatively analyze the member sensitivity of the temperature effect, the attenuation of material properties at elevated temperatures is considered. The yield stress of steel at temperature T is introduced into Equation (1), and the sensitivity formula of the member at a high temperature can be expressed as Equation (2):

$${\mathrm{SI}}_{ij}=\frac{{\sigma }_j^{\left(k+1\right)}-{\sigma }_j^{\left(k\right)}}{f_s^T-\left|{\sigma }_j^{\left(k\right)}\right|}$$

(2)

where $\sigma$ is the maximum principal stress of the member section, which is a function varying with the temperature T; subscript i is the number of the member at elevated temperature, j is the number of other members at room temperature, and $i\ne j$; k is the number of load steps; ${\sigma }_j^{\left(k\right)}$ is the stress calculated up to the kth step while member j at temperature T, $f_s^T$ is the yield stress at temperature T. $f_s^T-\left|{\sigma }_j^{\left(k\right)}\right|$ represents the stress margin of member j at temperature T, which is a constant positive value. ${\sigma }_j^{\left(k+1\right)}-{\sigma }_j^{\left(k\right)}$ represents the stress increment of member j from step k to step k + 1.

SI is a ratio of the stress increment to the stress margin, and the value range is (−1.0, 1.0); the larger the value is, the greater the member tends to be in a fully stressed state, and the smaller the capacity to continue bearing. When SI is greater than 1.0, it indicates the strength failure of member j. It is a mathematical certainty that the value of SI is a slope, which is the change rate of sensitivity with temperature. For the calculation results, SI can be either positive or negative; when SI > 0, it indicates that the internal force of the member will bear more load in the process of internal force redistribution; when SI < 0, it is a process of internal force release.

3. Finite Element Implementation

3.1. Model Design of Latticed Shell Structure

To find the changeable rule of member sensitivity with temperature when a structure is subjected to fire and then determine the influence of temperature on the progressive collapse-resisting performance of the spatial structure, a K8 single-layer latticed shell structure is taken as the research object, as shown in Figure 1. The structural span D = 32 m, the height h = 4 m, the members use a circular steel tube $\varphi$ 114 × 3, the live load is 0.5 kN/m², and the dead load is 0.5 kN/m².

3.2. Material Properties

The material is steel Q235B, and the values of the material parameters are taken according to the Code for fire safety of steel structures in buildings (GB512479-2017) [20]. The density is 7850 kg/m³, Poisson’s ratio is 0.3, coefficient of thermal expansion is $1.4\times {10}^{-5}$, and the elastic modulus at room temperature is 206 GPa. The reduction coefficient ${\xi }_{\mathrm{T}}$ of the elastic modulus when the temperature ranges from 20 to 600 °C is shown in Equation (3).

$${\xi }_{\mathrm{T}}=\frac{7T_{\mathrm{s}}-4780}{6T_{\mathrm{s}}-4760}$$

(3)

where $T_{\mathrm{s}}$ is the temperature of the steel. The stress-strain relationship of steel at the elevated temperature is an elastic-plastic isotropic strengthening model; strengthening and neck shrinkage are ignored [21]. The multilinear kinematic hardening model is selected in ANSYS. The stress-strain relationships of steel at different temperatures are shown in Figure 2.

3.3. Loading System

The temperature action is according to the ISO 834 standard heating curve, and the expression is

$$T_g-T_0=345\lg \left(8t+1\right)$$

(4)

where $T_g$ is the member temperature at time t; $T_0$ is the initial temperature of the member; t is the fire duration time.

According to Reference [20], the section shape factor of circle tube $\varphi$ 114 × 3 is greater than 300; therefore, the steel temperature can be equal to the air temperature.

3.4. Finite Element Model

The finite element model is established by ANSYS; Beam188 is used to simulate the members, which is based on Timoshenko beam theory; it is well-suited for simulating the members of the latticed shell structure. The nodes are rigid connections; the bottom nodes are simply supported. The initial geometric defect is applied by the first-order mode of the structure. The large geometric deformation is turned on in the calculation. Temperature loads are applied to the structure in the form of body loads. Set multiple load steps with temperature changes, and the temperature value is set every minute according to ISO834. The FE model is shown in Figure 3.

4. Test Results

The positions of accidental loads are random, and the affected members are also uncertain. Due to the large number of members of the lattice shell structure, it is very important to traverse and calculate all members. In this study, the characteristic members are selected, and a temperature load is applied to one member to analyze the response law of other members of the structure. According to the symmetry of the latticed shell structure, the half-side structure is taken as a schematic, and the number of each member is shown in Figure 4.

4.1. Effect of Temperature on Radial Ribs

Taking the radial rib as the analysis object, which is the main force transmission member in a single-layer latticed shell structure, the sensitivity of each member of the structure when one radial rib is heated is calculated. Three analysis conditions were designed in which radial ribs L73, L85, and L121 were heated. The first condition is that L73 is subjected to temperature, and the temperature variation range is from 20 °C to 500 °C. The other conditions are similar to explore the influence of heating of different radial ribs on the whole structure.

Take condition 1 for analysis. Applying a temperature load on member L73, the temperature function is according to Equation (4); the sensitivity coefficient of each member at the temperature load of each step is calculated using Equation (2). The calculation results of member sensitivity at different temperatures are marked in Figure 5.

As shown in Figure 5, it can ignore the effect of member sensitivity marked 0.0000, which is the calculated value is less than ${10}^{-5}$. When member L73 is subjected to a temperature load, from the radial point, the farther away from the elevated temperature member, the larger the value of the sensitivity coefficient. This indicates that members L85 and L121 bear the additional force generated during L73 heating up, and their own compressive stress decreases. From the circumferential point, the sensitivity values of radial ribs L74 and L76 change greatly, and L74 is the main forced member when the L73 temperature rises over 200 °C. The value of the circular ribs is tiny, which indicates that the circular ribs have less effect in the process of internal force redistribution. The above analysis shows that the radial members are the main forced members when radial ribs are subjected to fire.

The variation law of sensitivity with the temperature of circumferential ribs is shown in Figure 6.

As shown in Figure 5, the change trend of each circumferential rib is the same, and the sensitivity decreases with increasing temperature. The curve can be divided into three stages. In the first stage, the temperature is between 20 °C and 270 °C, the member sensitivity coefficient decreases linearly, and the stress increment of the adjacent member decreases. The main reason is that the axial force caused by the external load decreases due to thermal stress. In the second stage, between 270 °C and 400 °C, the curve drops sharply, and there are multiple inflection points in the fluctuation curve. The main reason is that the elastic modulus of steel decreases at the elevated temperature, and the stress increment decreases from step k to step k + 1, indicating that the internal force flow of the structure is the most significant when the member temperature rises in this range. In the third stage, the value of member sensitivity changes from positive to negative, and the value is small, which indicates that other members are not sensitive to L73 when the temperature increases over 400 °C. It can be considered that internal force redistribution has been completed.

To study the different fire-receiving elements on the longitudinal ribs, radial ribs L73, L85, and L121 were selected to heat up for analysis. Taking member L136 as the analysis object, the change curve of member sensitivity is shown in Figure 7.

As shown in Figure 7, the member near the vertex is more sensitive than the member near the supports. The reason is that the force of member L121 can be directly transmitted to supports, so member sensitivity is a kind of member with less influence in the transmission process of internal force.

4.2. Effect of Temperature on Ring Ribs

From the geometric point of view, the latticed shell structure is a perfectly symmetric structure, and it is representative of analyzing any circumferential member. Heating member L1, which is located at the first circular ribs, is heated to 500 °C. The sensitivity coefficients of the circumferential ribs, radial ribs, and diagonal braces are calculated and marked in Figure 8.

As shown in Figure 8, there is an inverse correlation with the distance between members and member L1, which heats up. The member is much closer to L1, the greater the sensitivity value, which indicates that the sensitivity value in the first quadrant is greater than members in the second quadrant; the sensitivity of radial ribs in the first ring is greater than members in the second ring.

The member sensitivity coefficients with temperatures of L2~L7 in the first ring are shown in Figure 9.

As shown in Figure 8 and Figure 9, the following conclusions can be drawn:

(1)

The sensitivity of members L2~L7 in the first ring increases with temperature. The sensitivity of member L2 adjacent to L1 has a maximum value, and member L4, which is perpendicular to L1, has the smallest sensitivity. This indicates that in the process of internal force redistribution, the elastic modulus of member L1 keeps decreasing with increasing temperature, the bearing capacity of member L1 decreases, member L2 adjacent to member L1 needs to bear more internal force, and is greatly affected by temperature and more dangerous under the elevated temperature. There is a rule for the sensitivity of radial ribs that the sensitivity is larger with the angle between the member and member in fire from 0° to 90°; the sensitivity decreases from 90° to 180°. This shows that during the process of inertial force redistribution, not only the members in the same direction as the load-bearing member but also members in other directions are affected.

(2)

Compared with circumferential members, the sensitivity coefficient of the radial rib is smaller, which indicates that the members on the same ring are the main force transmission member when one circumferential member is heated up, and the distal members are less affected.

(3)

Between 400 °C and 500 °C, there are inflection points in the curve of the sensitivity coefficient with increasing temperature, and the inflection points are consistent with the inflection point of the mechanical properties of steel.

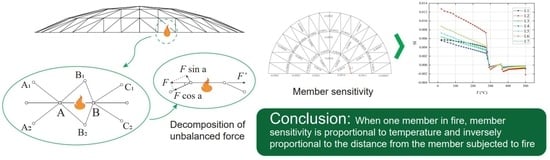
5. Load Path of Member under Elevated Temperature

The form of the single-layer latticed shell structure is an arch, and the members mainly bear axial compression under the action of external loads. The local structure is taken as the analysis component, which is composed of one node and six connected members, as shown in Figure 10.

As shown in Figure 10, assuming that member AB is in fire, the unbalanced forces F and F’ are generated by the thermal effect at both ends of the member nodes, as shown in Figure 11a. The deformation of points A and B is constrained by other members, and the unbalanced forces F and F’ are transmitted to adjacent members through the nodes. A schematic diagram of force decomposition is shown in Figure 11b; the force component $F_{\mathrm{y}}=F \cos \theta$ causes an increase in inertial force in OA, and $F_{\mathrm{x}}=F \sin \theta$ causes a shear force and a bending moment. The shear force $F_{\mathrm{y}}$ causes the upward displacement of point A. According to the same analysis, member BC can generate additional internal forces, and point B produces upward displacement. This process is the redistribution of local internal forces under temperature effects.

The unbalanced force generated by member AB is transmitted to adjacent members, and the radial component of force transfers to the next ring along BC, BC1, and BC2. The internal force change of a single member causes internal force flow in a local zone, and the change effect decreases with the increase in participating members. According to the analysis in Section 3, there is a certain range of the internal force redistribution of the latticed shell structure rather than the participation of all members of the structure, which can result from the latticed shell structure having a number of indeterminateness and high structural redundancy.

Generally, only one member failure is considered in current domestic and foreign design codes and guidelines for progressive collapse-resistant building structures. Different from static loads, members are more likely to buckle or be damaged in the condition of extreme fire disasters. When a structure is exposed to fire for a long time, one or more members of a latticed shell structure are prone to failure, resulting in progressive collapse because local members fail. This study analyses the flow direction of the internal force when the structure is in fire, determines the main forced transition member and load path, and analyses the most sensitive member. The results can provide a method to analyze the progressive collapse resistance of a single-layer latticed shell structure under fire disasters.

6. Discussion and Conclusions

A novel method to explore the law of redistribution of internal forces of Kiewitt reticulated shell structure under fire, the member sensitivity index, and the load path of members in the condition of a single member subjected to fire are studied. The following conclusions are obtained:

• A member sensitivity formula is proposed, which considers the temperature effect by introducing the yield stress of steel at elevated temperature; it can estimate the sensitivity of members to temperature by calculating the stress increment to evaluate the allowance of the members bearing capacity.
• The rule of member sensitivity with temperature is explored in the condition of radial ribs and circumferent ribs subjected to fire; the analysis reveals that member sensitivity increases with temperature; the farther away from the member subjected to fire, the smaller the member sensitivity. The additional internal force generated by one member subjected to fire is mainly borne by adjacent members, and the force will transmit along the member with higher sensitivity by changing the internal force of members in a local zone to make the structure reach a new equilibrium condition, the law of internal force redistribution is clarified when the structure is in fire.
• We proposed a prediction method proposed in this study; the sensitivity index is the difference calculation of stress from step k to step k + 1. The smaller the sensitivity coefficient is, the smaller the allowable bearing allowance of the member. In the condition of part of the structure subjected to fire, the maximum load path of the latticed shell structure can be determined, and the members that are prone to damage can be identified. This work provides a new idea for the analysis of resisting progressive collapse performance of a structure subjected to fire.