Explanation for the Multi-Component Scintillation of Cerium Fluoride Through the Equilibrium and Photophysical Investigation of Cerium(III)-Fluoro Complexes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents and Solutions
2.2. Instruments and Procedures
3. Results and Discussion
3.1. Absorption Spectra and Equilibria
3.2. Emission and Excitation Spectra
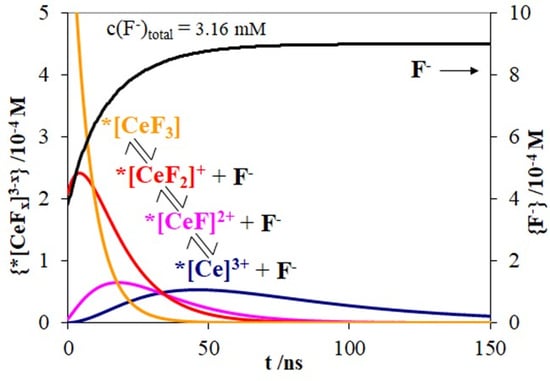
3.3. The Decays of Excited States
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Faschinger, F.; Ertl, M.; Zimmermann, M.; Horner, A.; Himmelsbach, M.; Schöfberger, W.; Knör, G.; Gruber, H.J. Stable Europium(III) Complexes with Short Linkers for Site-Specific Labeling of Biomolecules. ChemistryOpen 2017, 6, 721–732. [Google Scholar] [CrossRef] [PubMed]
- Bodył, S. Luminescence properties of Ce3+ and Eu2+ in fluorites and apatites. Mineralogia 2009, 40, 85–94. [Google Scholar] [CrossRef]
- Malchukova, E.; Boizot, B. Tunable luminescence from Ce-doped aluminoborosilicate glasses. J. Rare Earths 2014, 32, 217–220. [Google Scholar] [CrossRef] [Green Version]
- Jacobsohn, L.G.; Sprinkle, K.B.; Roberts, S.A.; Kucera, C.J.; James, T.L.; Yukihara, E.G.; DeVol, T.A.; Ballato, J. Fluoride Nanoscintillators. J. Nanomater. 2011, 2011, 523638. [Google Scholar] [CrossRef]
- Jacobsohn, L.G.; Toncelli, A.; Sprinkle, K.B.; Kucera, C.J.; Ballato, J. Spectral engineering of LaF3: Ce3+ nanoparticles: The role of Ce3+ in surface sites. J. Appl. Phys. 2012, 111, 074315. [Google Scholar] [CrossRef]
- Karimi, M.; Raeisi, M.; Bagherzadeh, M.; Payami, F. Enhancement in photoluminescence properties of organic compound PS/PPO by cerium fluoride nanoparticles doping. SN Appl. Sci. 2019, 1, 635. [Google Scholar] [CrossRef] [Green Version]
- Cooper, D.R.; Kudinov, K.; Tyagi, P.; Hill, C.K.; Bradforth, S.E.; Nadeau, J.L. Photoluminescence of cerium fluoride and cerium-doped lanthanum fluoride nanoparticles and investigation of energy transfer to photosensitizer molecules. Phys. Chem. Chem. Phys. 2014, 16, 12441–12453. [Google Scholar] [CrossRef]
- Shendrik, R.; Radzhabov, E.A.; Nepomnyashchikh, A.I. Scintillation properties of pure and Ce3+-doped SrF2 crystals. Radiat. Meas. 2013, 56, 58–61. [Google Scholar] [CrossRef]
- Shendrik, R.Y.; Radzhabov, E.A.; Nepomnyashchikh, A.I. Scintillation properties of SrF2 and SrF2-Ce3+ crystals. Tech. Phys. Lett. 2013, 39, 587–590. [Google Scholar] [CrossRef]
- Parmentier, A.; Smet, P.; Poelman, D. Broadband Luminescence in Rare Earth Doped Sr2SiS4: Relating Energy Levels of Ce3+ and Eu2+. Materials (Basel) 2013, 6, 3663–3675. [Google Scholar] [CrossRef]
- Ghamami, S.; Kazemzade Anari, S.; Bakhshi, M.; Lashgari, A.; Salgado-Morán, G.; Glossman-Mitnik, D. Preparation and Characterization of Cerium(III) Doped Captopril Nanoparticles and Study of their Photoluminescence Properties. Open Chem. 2016, 14, 60–64. [Google Scholar] [CrossRef]
- Oczko, G.; Macalik, L.; Legendziewicz, J.; Hanuza, J. Comparison of the spectroscopic behaviour of single crystals of lanthanide halides (X = Cl, Br). J. Alloys Compd. 2004, 380, 327–336. [Google Scholar] [CrossRef]
- Keller, B.; Legendziewicz, J.; Gliński, J. Investigation of optical properties of praseodymium and cerium chlorides in nonaqueous solutions. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1998, 54, 2207–2213. [Google Scholar] [CrossRef]
- Keller, B.; Legendziewicz, J.; Przybylski, J.; Guzik, M.; Gliński, J. Spectroscopic studies of lanthanide (Ce, Eu) chlorides in ethane-1,2-diol. J. Alloys Compd. 2002, 341, 197–202. [Google Scholar] [CrossRef]
- Glukhov, R.A.; Belsky, A.N.; Pedrini, C.; Vasil’ev, A.N. Simulation of energy conversion and transfer in CeF3 after VUV photon absorption. J. Alloys Compd. 1998, 275–277, 488–492. [Google Scholar] [CrossRef]
- Vogler, A.; Kunkely, H. Excited state properties of lanthanide complexes: Beyond ff states. Inorg. Chim. Acta 2006, 359, 4130–4138. [Google Scholar] [CrossRef]
- Anderson, D.F. Cerium fluoride: A scintillator for high-rate applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1990, 287, 606–612. [Google Scholar] [CrossRef]
- Pedrini, C.; Moine, B.; Bouttet, D.; Belsky, A.N.; Mikhailin, V.V.; Vasil’ev, A.N.; Zinin, E.I. Time-resolved luminescence of CeF3 crystals excited by X-ray synchrotron radiation. Chem. Phys. Lett. 1993, 206, 470–474. [Google Scholar] [CrossRef]
- Thoma, E.D.; Shields, H.; Zhang, Y.; McCollum, B.C.; Williams, R.T. EPR and luminescence studies of LaF3 and CeF3 under X-ray and laser irradiation. J. Lumin. 1997, 71, 93–104. [Google Scholar] [CrossRef]
- Lindner, R.; Reichling, M.; Matthias, E.; Johansen, H. Luminescence and damage thresholds of cerium-doped LaF3 for ns-pulsed laser excitation at 248 nm. Appl. Phys. B 1999, 68, 233–241. [Google Scholar] [CrossRef]
- Miskolczy, Z.; Biczók, L. Sequential inclusion of two berberine cations in cucurbit[8]uril cavity: Kinetic and thermodynamic studies. Phys. Chem. Chem. Phys. 2014, 16, 20147–20156. [Google Scholar] [CrossRef] [PubMed]
- Imran, M.; Kiss, M.; Valicsek, Z.; Horváth, O. Formation, Photophysics and Photochemistry of Anionic Lanthanide(III) Mono- and Bisporphyrins. Molecules 2019, 24, 1309. [Google Scholar] [CrossRef] [PubMed]
- Zékány, L.; Nagypál, I.; Peintler, G. Manual for PSEQUAD Version 5.01; University of Szeged and University of Debrecen: Szeged and Debrecen, Hungary, 2001. [Google Scholar]
- Peintler, G.; Nagypál, I.; Jancsó, A.; Epstein, I.R.; Kustin, K. Extracting Experimental Information from Large Matrixes. 1. A New Algorithm for the Application of Matrix Rank Analysis. J. Phys. Chem. A 1997, 101, 8013–8020. [Google Scholar] [CrossRef]
- Eaton, D.F. International union of pure and applied chemistry organic chemistry division commission on photochemistry. J. Photochem. Photobiol. B Biol. 1988, 2, 523–531. [Google Scholar] [CrossRef]
- Rabek, J.F. Experimental Methods in Photochemistry and Photophysics (Parts I and II); Wiley-Interscience publication, John Wiley and Sons, Ltd.: Chichester, UK, 1982. [Google Scholar]
- Demas, J.N. Excited State Lifetime Measurements; Academic Press Inc.: Cambridge, MA, USA, 1983. [Google Scholar]
- Fodor, L.; Horváth, A. Characterization of exciplexes generated by excited tris-diimine—Ruthenium(II) complexes and silver(I) ion of ground state. J. Photochem. Photobiol. A Chem. 1998, 112, 213–223. [Google Scholar] [CrossRef]
- Peintler, G. Reference Manual ZITA Version 4.1; A Comprehensive Program Package for Fitting Parameters of Chemical Reaction Mechanisms; Attila József University: Szeged, Hungary, 1977. [Google Scholar]
- Kovács, M.; Valicsek, Z.; Tóth, J.; Hajba, L.; Makó, É.; Halmos, P.; Földényi, R. Multi-analytical approach of the influence of sulphate ion on the formation of cerium(III) fluoride nanoparticles in precipitation reaction. Colloids Surf. A Physicochem. Eng. Asp. 2009, 352, 56–62. [Google Scholar] [CrossRef]
- Lee, J.H.; Byrne, R.H. Rare earth element complexation by fluoride ions in aqueous solution. J. Solut. Chem. 1993, 22, 751–766. [Google Scholar] [CrossRef]
- Menon, M.P.; James, J. Solubilities, solubility products and solution chemistry of lanthanon trifluoride–water systems. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1989, 85, 2683. [Google Scholar] [CrossRef]
- Luo, Y.; Millero, F.J. Effects of temperature and ionic strength on the stabilities of the first and second fluoride complexes of yttrium and the rare earth elements. Geochim. Cosmochim. Acta 2004, 68, 4301–4308. [Google Scholar] [CrossRef]
- Luo, Y.-R.; Byrne, R.H. The Influence of Ionic Strength on Yttrium and Rare Earth Element Complexation by Fluoride Ions in NaClO4, NaNO3 and NaCl Solutions at 25 °C. J. Solut. Chem. 2007, 36, 673–689. [Google Scholar] [CrossRef]
- Svetashev, A.G.; Tsvirko, M.P. Influence of temperature on spectral-luminescent properties of trivalent cerium salts. Theor. Exp. Chem. 1985, 20, 653–658. [Google Scholar] [CrossRef]
- Moses, W.W.; Derenzo, S.E.; Weber, M.J.; Ray-Chaudhuri, A.K.; Cerrina, F. Scintillation mechanisms in cerium fluoride. J. Lumin. 1994, 59, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, M.; Ishii, M.; Krivandina, E.A.; Litvinov, M.M.; Peresypkin, A.I.; Prokoshkin, Y.D.; Rykalin, V.I.; Sobolev, B.P.; Takamatsu, K.; Vasil’chenko, V.G. Cerium fluoride, a highly radiation-resistive scintillator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1991, 302, 443–446. [Google Scholar] [CrossRef]
- Marrone, S.; Berthomieux, E.; Becvar, F.; Cano-Ott, D.; Colonna, N.; Domingo-Pardo, C.; Gunsing, F.; Haight, R.C.; Heil, M.; Käppeler, F.; et al. Pulse shape analysis of signals from BaF2 and CeF3 scintillators for neutron capture experiments. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 568, 904–911. [Google Scholar] [CrossRef]
- Víllora, E.G.; Shimamura, K.; Nakakita, S.; Nikl, M.; Ichinose, N. Scintillation properties of REF3 (RE = Ce, Pr, Nd) single crystals. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2005, 537, 139–143. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, G.; Poulain, M. Cerium-containing glasses for fast scintillators. J. Alloys Compd. 1998, 275–277, 733–737. [Google Scholar] [CrossRef]
- Kobayashi, M.; Ishii, M.; Sobolev, B.; Zhmurova, Z.; Krivandina, E. Scintillation characteristics of nonstoichiometric phases formed in MF2–GdF3–CeF3 system Part I. (M = Ba), scintillation of Ba0.9Gd0.1−xCexF2.1 (0 ≤ x ≤ 0.1) fluorite-type crystals. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1999, 421, 180–190. [Google Scholar] [CrossRef]
- Guillot-Noël, O.; de Haas, J.T.M.; Dorenbos, P.; van Eijk, C.W.E.; Krämer, K.; Güdel, H.U. Optical and scintillation properties of cerium-doped LaCl3, LuBr3 and LuCl3. J. Lumin. 1999, 85, 21–35. [Google Scholar] [CrossRef]







| Complex | [Ce]3+ | [CeF]2+ | [CeF2]+ | [CeF3] |
|---|---|---|---|---|
| lgβx | - | 6.49 | 11.46 | 15.45 |
| lg*βx | - | 3.34 | 5.18 | 6.03 |
| λ1/nm | 296 | 294 | (290) | 265 |
| ε1/M−1cm−1 | 16.5 | 10.1 | (0.0) | 82.4 |
| shift1/cm−1 | - | 195 | 693 | 3890 |
| λ2/nm | 251 | 250 | 248 | 247 |
| ε2/M−1cm−1 | 738 | 669 | 674 | 663 |
| shift2/cm−1 | - | 242 | 610 | 754 |
| λ3/nm | 237 | 235 | 233 | 232 |
| ε3/M−1cm−1 | 523 | 391 | 312 | 420 |
| shift3/cm−1 | - | 195 | 622 | 848 |
| λ4/nm | 221 | 220 | 218 | 217 |
| ε4/M−1cm−1 | 390 | 331 | 341 | 380 |
| shift4/cm−1 | - | 169 | 519 | 780 |
| λ5/nm | 210 | 209 | 206 | 206 |
| ε5/M−1cm−1 | 241 | 146 | 165 | 207 |
| shift5/cm−1 | - | 153 | 831 | 972 |
| crystal-field splitting/cm−1 | 13,818 | 13,776 | (13,957) | 10,900 |
| Complex | [Ce]3+ | [CeF]2+ | [CeF2]+ | [CeF3] |
|---|---|---|---|---|
| λ1/nm | 358 | 356 | 348 | 327 |
| shift/cm−1 | - | 175 | 829 | 2641 |
| Stokes/cm−1 | 5872 | 5892 | 5736 | 7122 |
| Φr | 0.990 | 0.769 | 0.604 | 0.377 |
| Complex | kd,i/107 s−1 | *ki+/107 M−1 s−1 | *ki−/107 s−1 | lg*Ki/M−1 |
|---|---|---|---|---|
| [Ce]3+ | 1.98 | - | - | - |
| [CeF]2+ | 2.83 | 0.348 | 3.80 | −1.04 |
| [CeF2]+ | 4.81 | 0.0915 | 3.04 | −1.52 |
| [CeF3] | 9.84 | 120 | 4.43 | 1.43 |
| Complex | [Ce]3+ | [CeF]2+ | [CeF2]+ | [CeF3] |
|---|---|---|---|---|
| Φr | 0.990 | 0.769 | 0.604 | 0.377 |
| τ/ns | 50.6 | 35.3 | 20.8 | 10.2 |
| kr/107 s−1 | 1.96 | 2.18 | 2.91 | 3.71 |
| knr/107 s−1 | 0.0198 | 0.654 | 1.90 | 6.13 |
| τ0 = 1/kr/ns | 51.1 | 45.9 | 34.4 | 27.0 |
| kd = 1/τ/107 s−1 | 1.98 | 2.83 | 4.81 | 9.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valicsek, Z.; Kovács, M.; Horváth, O. Explanation for the Multi-Component Scintillation of Cerium Fluoride Through the Equilibrium and Photophysical Investigation of Cerium(III)-Fluoro Complexes. Nanomaterials 2019, 9, 1462. https://doi.org/10.3390/nano9101462
Valicsek Z, Kovács M, Horváth O. Explanation for the Multi-Component Scintillation of Cerium Fluoride Through the Equilibrium and Photophysical Investigation of Cerium(III)-Fluoro Complexes. Nanomaterials. 2019; 9(10):1462. https://doi.org/10.3390/nano9101462
Chicago/Turabian StyleValicsek, Zsolt, Máté Kovács, and Ottó Horváth. 2019. "Explanation for the Multi-Component Scintillation of Cerium Fluoride Through the Equilibrium and Photophysical Investigation of Cerium(III)-Fluoro Complexes" Nanomaterials 9, no. 10: 1462. https://doi.org/10.3390/nano9101462
APA StyleValicsek, Z., Kovács, M., & Horváth, O. (2019). Explanation for the Multi-Component Scintillation of Cerium Fluoride Through the Equilibrium and Photophysical Investigation of Cerium(III)-Fluoro Complexes. Nanomaterials, 9(10), 1462. https://doi.org/10.3390/nano9101462