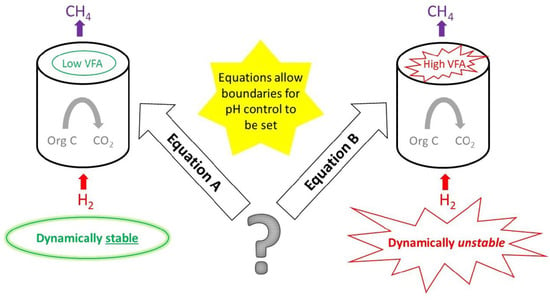
Validation of Two Theoretically Derived Equations for Predicting pH in CO2 Biomethanisation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Equations Relating pH and pCO2
2.2. Literature Data
2.3. Digester Set-Up and Operation
2.4. Analytical Methods
2.5. Performance Assessment and Statistical Analyses
3. Results
3.1. Application of Equation A to the Literature Data
3.2. Application of Equation B to the Literature Data
3.3. Application of Equations A and B to Multi-Point Data
3.4. Experimental Trial of H2 Addition to Induce Digestion Instability
3.4.1. Digestion Performance
3.4.2. VFA Profiles
3.5. Application of Equations A and B to Experimental Data
4. Discussion
4.1. Methodological Issues with Data in Literature Studies
4.2. General Research-Related Issues
4.3. Considerations for Large-Scale Operation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A









References
- Zeikus, J. The biology of methanogenic bacteria. Bacteriol. Rev. 1977, 41, 514–541. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Angelidaki, I. Integrated biogas upgrading and hydrogen utilization in an anaerobic reactor containing enriched hydrogenotrophic methanogenic culture. Biotechnol. Bioeng. 2012, 109, 2729–2736. [Google Scholar] [CrossRef] [PubMed]
- Rafrafi, Y.; Laguillaumie, L.; Dumas, C. Biological Methanation of H2 and CO2 with Mixed Cultures: Current Advances, Hurdles and Challenges. Waste Biomass Valorization 2020, 12, 5259–5282. [Google Scholar] [CrossRef]
- Zavarkó, M.; Imre, A.R.; Pörzse, G.; Csedő, Z. Past, Present and Near Future: An Overview of Closed, Running and Planned Biomethanation Facilities in Europe. Energies 2021, 14, 5591. [Google Scholar] [CrossRef]
- Aryal, N.; Kvist, T.; Ammam, F.; Pant, D.; Ottosen, L.D. An overview of microbial biogas enrichment. Bioresour. Technol. 2018, 264, 359–369. [Google Scholar] [CrossRef]
- Tao, B.; Zhang, Y.; Heaven, S.; Banks, C.J. Predicting pH rise as a control measure for integration of CO2 biomethanisation with anaerobic digestion. Appl. Energy 2020, 277, 115535. [Google Scholar] [CrossRef]
- Andreides, D.; Stransky, D.; Bartackova, J.; Pokorna, D.; Zabranska, J. Syngas biomethanation in countercurrent flow trickle-bed reactor operated under different temperature conditions. Renew. Energy 2022, 199, 1329–1335. [Google Scholar] [CrossRef]
- Ghofrani-Isfahani, P.; Tsapekos, P.; Peprah, M.; Kougias, P.; Zervas, A.; Zhu, X.; Yang, Z.; Jacobsen, C.S.; Angelidaki, I. Ex-Situ biogas upgrading in thermophilic trickle bed reactors packed with micro-porous packing materials. Chemosphere 2022, 296, 133987. [Google Scholar] [CrossRef]
- Paniagua, S.; Lebrero, R.; Muñoz, R. Syngas biomethanation: Current state and future perspectives. Bioresour. Technol. 2022, 358, 127436. [Google Scholar] [CrossRef]
- Dong, D.; Choi, O.K.; Lee, J.W. Influence of the continuous addition of zero valent iron (ZVI) and nano-scaled zero valent iron (nZVI) on the anaerobic biomethanation of carbon dioxide. Chem. Eng. J. 2022, 430, 132233. [Google Scholar] [CrossRef]
- Geppert, F.; Liu, D.; van Eerten-Jansen, M.; Weidner, E.; Buisman, C.; Ter Heijne, A. Bioelectrochemical power-to-gas: State of the art and future perspectives. Trends Biotechnol. 2016, 34, 879–894. [Google Scholar] [CrossRef]
- Bywater, A.; Heaven, S.; Zhang, Y.; Banks, C.J. Potential for Biomethanisation of CO2 from Anaerobic Digestion of Organic Wastes in the United Kingdom. Processes 2022, 10, 1202. [Google Scholar] [CrossRef]
- D’Silva, T.C.; Isha, A.; Chandra, R.; Vijay, V.K.; Subbarao, P.M.V.; Kumar, R.; Chaudhary, V.P.; Singh, H.; Khan, A.A.; Tyagi, V.K. Enhancing methane productionh in anaerobic digestion through hydrogen assisted pathways—A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 151, 111536. [Google Scholar] [CrossRef]
- Lai, C.S.; McCulloch, M.D. Sizing of stand-alone solar PV and storage system with anaerobic digestion biogas power plants. IEEE Trans. Ind. Electron. 2016, 64, 2112–2121. [Google Scholar] [CrossRef]
- Wang, P.; Wang, J.; Jin, R.; Li, G.; Zhou, M.; Xia, Q. Integrating biogas in regional energy systems to achieve near-zero carbon emissions. Appl. Energy 2022, 322, 119515. [Google Scholar] [CrossRef]
- Angelidaki, I.; Treu, L.; Tsapekos, P.; Luo, G.; Campanaro, S.; Wenzel, H.; Kougias, P.G. Biogas upgrading and utilization: Current status and perspectives. Biotechnol. Adv. 2018, 36, 452–466. [Google Scholar] [CrossRef] [Green Version]
- Luo, G.; Angelidaki, I. Co-digestion of manure and whey for in situ biogas upgrading by the addition of H2: Process performance and microbial insights. Appl. Microbiol. Biotechnol. 2013, 97, 1373–1381. [Google Scholar] [CrossRef]
- Luo, G.; Johansson, S.; Boe, K.; Xie, L.; Zhou, Q.; Angelidaki, I. Simultaneous hydrogen utilization and in situ biogas upgrading in an anaerobic reactor. Biotechnol. Bioeng. 2012, 109, 1088–1094. [Google Scholar] [CrossRef]
- Drosg, B. Process Monitoring in Biogas Plants; IEA Bioenergy: Paris, France, 2013. [Google Scholar]
- Gaida, D.; Wolf, C.; Bongards, M. Feed control of anaerobic digestion processes for renewable energy production: A review. Renew. Sustain. Energy Rev. 2017, 68, 869–875. [Google Scholar] [CrossRef]
- Nguyen, D.; Gadhamshetty, V.; Nitayavardhana, S.; Khanal, S.K. Automatic process control in anaerobic digestion technology: A critical review. Bioresour. Technol. 2015, 193, 513–522. [Google Scholar] [CrossRef]
- Wade, M.J. Not just numbers: Mathematical modelling and its contribution to anaerobic digestion processes. Processes 2020, 8, 888. [Google Scholar] [CrossRef]
- Tao, B.; Alessi, A.M.; Zhang, Y.; Chong, J.P.; Heaven, S.; Banks, C.J. Simultaneous biomethanisation of endogenous and imported CO2 in organically loaded anaerobic digesters. Appl. Energy 2019, 247, 670–681. [Google Scholar] [CrossRef]
- APHA. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2005. [Google Scholar]
- Ripley, L.E.; Boyle, W.C.; Converse, J.C. Improved alkalimetric monitoring for anaerobic digestion of high-strength wastes. J. (Water Pollut. Control Fed.) 1986, 58, 406–411. [Google Scholar]
- Walker, M.; Zhang, Y.; Heaven, S.; Banks, C. Potential errors in the quantitative evaluation of biogas production in anaerobic digestion processes. Bioresour. Technol. 2009, 100, 6339–6346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, D.; Li, L.; Zhao, X.; Peng, Y.; Yang, P.; Peng, X. Anaerobic digestion: A review on process monitoring. Renew. Sustain. Energy Rev. 2019, 103, 1–12. [Google Scholar] [CrossRef]
- Agneessens, L.M.; Ottosen, L.D.M.; Andersen, M.; Olesen, C.B.; Feilberg, A.; Kofoed, M.V.W. Parameters affecting acetate concentrations during in-situ biological hydrogen methanation. Bioresour. Technol. 2018, 258, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Agneessens, L.M.; Ottosen, L.D.M.; Voigt, N.V.; Nielsen, J.L.; de Jonge, N.; Fischer, C.H.; Kofoed, M.V.W. In-situ biogas upgrading with pulse H2 additions: The relevance of methanogen adaption and inorganic carbon level. Bioresour. Technol. 2017, 233, 256–263. [Google Scholar] [CrossRef] [PubMed]
- Alfaro, N.; Fdz-Polanco, M.; Fdz-Polanco, F.; Díaz, I. H2 addition through a submerged membrane for in-situ biogas upgrading in the anaerobic digestion of sewage sludge. Bioresour. Technol. 2019, 280, 1–8. [Google Scholar] [CrossRef]
- Andreides, D.; Pokorna, D.; Zabranska, J. Assessing the syngas biomethanation in anaerobic sludge digestion under different syngas loading rates and homogenisation. Fuel 2022, 320, 123929. [Google Scholar] [CrossRef]
- Bassani, I.; Kougias, P.G.; Treu, L.; Angelidaki, I. Biogas upgrading via hydrogenotrophic methanogenesis in two-stage continuous stirred tank reactors at mesophilic and thermophilic conditions. Environ. Sci. Technol. 2015, 49, 12585–12593. [Google Scholar] [CrossRef]
- Corbellini, V.; Catenacci, A.; Malpei, F. Hydrogenotrophic biogas upgrading integrated into WWTPs: Enrichment strategy. Water Sci. Technol. 2019, 79, 759–770. [Google Scholar] [CrossRef] [PubMed]
- Corbellini, V.; Feng, C.; Bellucci, M.; Catenacci, A.; Stella, T.; Espinoza-Tofalos, A.; Malpei, F. Performance Analysis and Microbial Community Evolution of In Situ Biological Biogas Upgrading with Increasing H2/CO2 Ratio. Archaea 2021, 2021, 8894455. [Google Scholar] [CrossRef] [PubMed]
- Díaz, I.; Fdz-Polanco, F.; Mutsvene, B.; Fdz-Polanco, M. Effect of operating pressure on direct biomethane production from carbon dioxide and exogenous hydrogen in the anaerobic digestion of sewage sludge. Appl. Energy 2020, 280, 115915. [Google Scholar] [CrossRef]
- Khan, A.; Akbar, S.; Okonkwo, V.; Smith, C.; Khan, S.; Shah, A.A.; Adnan, F.; Ijaz, U.Z.; Ahmed, S.; Badshah, M. Enrichment of the hydrogenotrophic methanogens for, in-situ biogas up-gradation by recirculation of gases and supply of hydrogen in methanogenic reactor. Bioresour. Technol. 2022, 345, 126219. [Google Scholar] [CrossRef]
- Kim, S.; Mostafa, A.; Im, S.; Lee, M.-K.; Kang, S.; Na, J.-G.; Kim, D.-H. Production of high-calorific biogas from food waste by integrating two approaches: Autogenerative high-pressure and hydrogen injection. Water Res. 2021, 194, 116920. [Google Scholar] [CrossRef]
- Lebranchu, A.; Blanchard, F.; Fick, M.; Pacaud, S.; Olmos, E.; Delaunay, S. Pilot-scale biomethanation of cattle manure using dense membranes. Bioresour. Technol. 2019, 284, 430–436. [Google Scholar] [CrossRef]
- Lovato, G.; Alvarado-Morales, M.; Kovalovszki, A.; Peprah, M.; Kougias, P.G.; Rodrigues, J.A.D.; Angelidaki, I. In-situ biogas upgrading process: Modeling and simulations aspects. Bioresour. Technol. 2017, 245, 332–341. [Google Scholar] [CrossRef] [Green Version]
- Luo, G.; Angelidaki, I. Hollow fiber membrane based H2 diffusion for efficient in situ biogas upgrading in an anaerobic reactor. Appl. Microbiol. Biotechnol. 2013, 97, 3739–3744. [Google Scholar] [CrossRef]
- Luo, G.; Wang, W.; Angelidaki, I. Anaerobic digestion for simultaneous sewage sludge treatment and CO biomethanation: Process performance and microbial ecology. Environ. Sci. Technol. 2013, 47, 10685–10693. [Google Scholar] [CrossRef]
- Treu, L.; Kougias, P.; de Diego-Díaz, B.; Campanaro, S.; Bassani, I.; Fernández-Rodríguez, J.; Angelidaki, I. Two-year microbial adaptation during hydrogen-mediated biogas upgrading process in a serial reactor configuration. Bioresour. Technol. 2018, 264, 140–147. [Google Scholar] [CrossRef]
- Treu, L.; Tsapekos, P.; Peprah, M.; Campanaro, S.; Giacomini, A.; Corich, V.; Kougias, P.G.; Angelidaki, I. Microbial profiling during anaerobic digestion of cheese whey in reactors operated at different conditions. Bioresour. Technol. 2019, 275, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Voelklein, M.; Rusmanis, D.; Murphy, J. Biological methanation: Strategies for in-situ and ex-situ upgrading in anaerobic digestion. Appl. Energy 2019, 235, 1061–1071. [Google Scholar] [CrossRef]
- Wahid, R.; Horn, S.J. Impact of operational conditions on methane yield and microbial community composition during biological methanation in in situ and hybrid reactor systems. Biotechnol. Biofuels 2021, 14, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Wahid, R.; Horn, S.J. The effect of mixing rate and gas recirculation on biological CO2 methanation in two-stage CSTR systems. Biomass Bioenergy 2021, 144, 105918. [Google Scholar] [CrossRef]
- Wahid, R.; Mulat, D.G.; Gaby, J.C.; Horn, S.J. Effects of H2:CO2 ratio and H2 supply fluctuation on methane content and microbial community composition during in-situ biological biogas upgrading. Biotechnol. Biofuels 2019, 12, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Xie, L.; Luo, G.; Zhou, Q.; Angelidaki, I. Performance and microbial community analysis of the anaerobic reactor with coke oven gas biomethanation and in situ biogas upgrading. Bioresour. Technol. 2013, 146, 234–239. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Liu, Y.; Zhang, J.; Mao, K.; Kurbonova, M.; Liu, G.; Zhang, R.; Wang, W. Improvement of biofuel recovery from food waste by integration of anaerobic digestion, digestate pyrolysis and syngas biomethanation under mesophilic and thermophilic conditions. J. Clean. Prod. 2020, 256, 120594. [Google Scholar] [CrossRef]
- Zhu, X.; Cao, Q.; Chen, Y.; Sun, X.; Liu, X.; Li, D. Effects of mixing and sodium formate on thermophilic in-situ biogas upgrading by H2 addition. J. Clean. Prod. 2019, 216, 373–381. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, L.; Chen, Y.; Cao, Q.; Liu, X.; Li, D. Differences of methanogenesis between mesophilic and thermophilic in situ biogas-upgrading systems by hydrogen addition. J. Ind. Microbiol. Biotechnol. 2019, 46, 1569–1581. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, L.; Chen, Y.; Cao, Q.; Liu, X.; Li, D. Effect of H2 addition on the microbial community structure of a mesophilic anaerobic digestion system. Energy 2020, 198, 117368. [Google Scholar] [CrossRef]
- Bassani, I.; Kougias, P.G.; Angelidaki, I. In-situ biogas upgrading in thermophilic granular UASB reactor: Key factors affecting the hydrogen mass transfer rate. Bioresour. Technol. 2016, 221, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Jing, Y.; Campanaro, S.; Kougias, P.; Treu, L.; Angelidaki, I.; Zhang, S.; Luo, G. Anaerobic granular sludge for simultaneous biomethanation of synthetic wastewater and CO with focus on the identification of CO-converting microorganisms. Water Res. 2017, 126, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Deschamps, L.; Imatoukene, N.; Lemaire, J.; Mounkaila, M.; Filali, R.; Lopez, M.; Theoleyre, M.-A. In-situ biogas upgrading by bio-methanation with an innovative membrane bioreactor combining sludge filtration and H2 injection. Bioresour. Technol. 2021, 337, 125444. [Google Scholar] [CrossRef]
- Hafuka, A.; Fujino, S.; Kimura, K.; Oshita, K.; Konakahara, N.; Takahashi, S. In-situ biogas upgrading with H2 addition in an anaerobic membrane bioreactor (AnMBR) digesting waste activated sludge. Sci. Total Environ. 2022, 828, 154573. [Google Scholar] [CrossRef] [PubMed]
- Illi, L.; Lecker, B.; Lemmer, A.; Müller, J.; Oechsner, H. Biological methanation of injected hydrogen in a two-stage anaerobic digestion process. Bioresour. Technol. 2021, 333, 125126. [Google Scholar] [CrossRef]
- Thapa, A.; Park, J.-G.; Yang, H.-M.; Jun, H.-B. In-situ biogas upgrading in an anaerobic trickling filter bed reactor treating a thermal post-treated digestate. J. Environ. Chem. Eng. 2021, 9, 106780. [Google Scholar] [CrossRef]
- Corbellini, V.; Kougias, P.G.; Treu, L.; Bassani, I.; Malpei, F.; Angelidaki, I. Hybrid biogas upgrading in a two-stage thermophilic reactor. Energy Convers. Manag. 2018, 168, 1–10. [Google Scholar] [CrossRef]
- Andreides, D.; Quispe, J.I.B.; Bartackova, J.; Pokorna, D.; Zabranska, J. A novel two-stage process for biological conversion of syngas to biomethane. Bioresour. Technol. 2021, 327, 124811. [Google Scholar] [CrossRef]
- Scholten, J.C.; Conrad, R. Energetics of syntrophic propionate oxidation in defined batch and chemostat cocultures. Appl. Environ. Microbiol. 2000, 66, 2934–2942. [Google Scholar] [CrossRef] [Green Version]
- Fontana, A.; Kougias, P.G.; Treu, L.; Kovalovszki, A.; Valle, G.; Cappa, F.; Morelli, L.; Angelidaki, I.; Campanaro, S. Microbial activity response to hydrogen injection in thermophilic anaerobic digesters revealed by genome-centric metatranscriptomics. Microbiome 2018, 6, 194. [Google Scholar] [CrossRef]
- Batstone, D.J.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.; Pavlostathis, S.; Rozzi, A.; Sanders, W.; Siegrist, H.; Vavilin, V. The IWA anaerobic digestion model no 1 (ADM1). Water Sci. Technol. 2002, 45, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Heaven, S.; Zhang, Y.; Bywater, A.; Banks, C. Dataset for ‘Potential for Biomethanisation of CO2 from Anaerobic Digestion of Organic Wastes in the UK’. 2022. Available online: https://eprints.soton.ac.uk/467644/1/processes_10_01202_1_.pdf (accessed on 6 June 2022).
- Palù, M.; Peprah, M.; Tsapekos, P.; Kougias, P.; Campanaro, S.; Angelidaki, I.; Treu, L. In-situ biogas upgrading assisted by bioaugmentation with hydrogenotrophic methanogens during mesophilic and thermophilic co-digestion. Bioresour. Technol. 2022, 348, 126754. [Google Scholar] [CrossRef] [PubMed]






| (i) | (ii) | (iii) | (iv) | (v) | (vi) | RMSD | R2 | ||
|---|---|---|---|---|---|---|---|---|---|
| No H2 | With H2 | No H2 | With H2 | No H2 | With H2 | ||||
| Temp | °C | 55 | 55 | 55 | 55 | 55 | 55 | - | - |
| OLR | g VS L−1 day−1 | 1.67 | 1.67 | 1.67 | 1.67 | 1.67 | 1.67 | - | - |
| HRT | days | 15 | 15 | 15 | 15 | 15 | 15 | - | - |
| H2 input | L L−1 day−1 | 0 | 0.93 | 0 | 1.44 | 0 | 1.76 | - | - |
| SMPtot | L CH4 g−1 VS | 0.275 | 0.407 | 0.271 | 0.478 | 0.287 | 0.515 | - | - |
| CH4 | % | 54.2 | 78.4 | 53.1 | 90.2 | 55.4 | 96.1 | - | - |
| TAN | M | n/r | n/r | n/r | n/r | n/r | n/r | - | - |
| VFA | M | 0.002 | 0.004 | 0.002 | 0.012 | 0.002 | 0.038 | - | - |
| pH | - | 7.29 | 7.61 | 7.28 | 7.9 | 7.3 | 8.31 | - | - |
| pCO2 | - | 0.458 | 0.216 | 0.469 | 0.098 | 0.446 | 0.039 | - | - |
| a × 108 | 10.41 | 9.81 | 10.42 | 9.81 | 10.43 | 6.99 | - | - | |
| Difference between experimental and predicted pH based on Equation A with coefficient a(x) | |||||||||
| a(i) | - | - | 0.02 | 0.00 | 0.02 | 0.00 | 0.12 | 0.06 | 0.997 |
| a(ii) | - | 0.02 | - | 0.02 | 0.00 | 0.02 | 0.10 | 0.05 | 0.997 |
| a(iii) | - | 0.00 | 0.02 | - | 0.02 | 0.00 | 0.12 | 0.06 | 0.997 |
| a(iv) | - | 0.02 | 0.00 | 0.02 | - | 0.02 | 0.10 | 0.05 | 1.000 |
| a(v) | - | 0.00 | 0.02 | 0.00 | 0.02 | - | 0.12 | 0.06 | 0.997 |
| a(vi) | - | 0.16 | 0.13 | 0.16 | 0.12 | 0.16 | - | 0.15 | 1.000 |
| (i) | (ii) | (iii) | (iv) | (v) | (vi) | (vii) | RMSD | R2 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Phase | 1 | 2 | 3a | 3b | 3c | 3d | 3e | |||
| H2/CO2 | 0 | 2 | 4 | 4 | 4 | 4 | 4 | |||
| Mixing | Rpm | 80 | 80 | 80 | 120 | 140 | 170 | 200 | - | - |
| Temp | °C | 55 | 55 | 55 | 55 | 55 | 55 | 55 | - | - |
| OLR | g VS L−1 day−1 | 3.09 | 2.69 | 2.30 | 2.36 | 2.19 | 2.37 | 2.32 | - | - |
| HRT | Days | 20 | 20 | 20 | 20 | 20 | 20 | 20 | - | - |
| H2 input | L L−1 day−1 | 0.0 | 0.8 | 1.6 | 1.7 | 1.7 | 1.7 | 1.7 | - | - |
| SMP total | L CH4 g−1 VS | 0.217 | 0.246 | 0.305 | 0.331 | 0.411 | 0.321 | 0.315 | - | - |
| CH4 | % | 62.2 | 37.8 | 31.6 | 38.3 | 40.3 | 41.9 | 40.2 | - | - |
| TAN | M | 0.10 | 0.11 | 0.13 | 0.15 | 0.14 | 0.14 | 0.14 | - | - |
| VFA | M | 0.005 | 0.006 | 0.008 | 0.011 | 0.012 | 0.016 | 0.015 | - | - |
| pH | - | 7.86 | 8.07 | 8.25 | 8.37 | 8.41 | 8.43 | 8.41 | - | - |
| pCO2 | - | 0.378 | 0.207 | 0.137 | 0.124 | 0.119 | 0.116 | 0.120 | - | - |
| a × 108 | - | 2.85 | 2.82 | 2.43 | 1.81 | 1.63 | 1.56 | 1.62 | - | - |
| b × 108 | - | 0.255 | 0.277 | 0.278 | 0.233 | 0.193 | 0.162 | 0.171 | - | - |
| Difference between experimental and predicted pH based on Equation A with coefficient a(x) | ||||||||||
| a(i) | - | - | 0.00 | 0.05 | 0.14 | 0.17 | 0.18 | 0.17 | 0.14 | 0.949 |
| a(ii) | - | 0.00 | - | 0.05 | 0.13 | 0.16 | 0.18 | 0.16 | 0.13 | 0.966 |
| a(iii) | - | 0.06 | 0.05 | - | 0.09 | 0.12 | 0.13 | 0.12 | 0.10 | 0.978 |
| a(iv) | - | 0.16 | 0.14 | 0.09 | - | 0.03 | 0.04 | 0.03 | 0.10 | 0.955 |
| a(v) | - | 0.19 | 0.17 | 0.12 | 0.03 | - | 0.01 | 0.00 | 0.12 | 0.956 |
| a(vi) | - | 0.21 | 0.19 | 0.13 | 0.04 | 0.01 | - | 0.01 | 0.13 | 0.958 |
| a(vii) | - | 0.19 | 0.18 | 0.12 | 0.03 | 0.00 | 0.01 | - | 0.12 | 0.957 |
| Difference between experimental and predicted pH based on Equation B with coefficient b(x) | ||||||||||
| b(i) | - | - | 0.03 | 0.03 | 0.03 | 0.08 | 0.12 | 0.11 | 0.08 | 0.853 |
| b(ii) | - | 0.03 | - | 0.00 | 0.05 | 0.10 | 0.15 | 0.13 | 0.09 | 0.940 |
| b(iii) | - | 0.03 | 0.00 | - | 0.05 | 0.10 | 0.15 | 0.13 | 0.09 | 0.963 |
| b(iv) | - | 0.03 | 0.06 | 0.05 | - | 0.05 | 0.10 | 0.08 | 0.07 | 0.941 |
| b(v) | - | 0.10 | 0.11 | 0.11 | 0.05 | - | 0.05 | 0.03 | 0.08 | 0.929 |
| b(vi) | - | 0.16 | 0.17 | 0.16 | 0.10 | 0.05 | - | 0.01 | 0.12 | 0.947 |
| b(vii) | - | 0.14 | 0.15 | 0.14 | 0.09 | 0.03 | 0.01 | - | 0.11 | 0.942 |
| OLR 3 | (i) | (ii) | (iii) | (iv) | (v) | (vi) | RMSD | R2 | |
|---|---|---|---|---|---|---|---|---|---|
| Phase | 1 | 2 | 3 | ||||||
| No H2 | No H2 | With H2 | With H2 | H2 + CO2 | H2 + CO2 | ||||
| Temp | °C | 37 | 37 | 37 | 37 | 37 | 37 | - | - |
| OLR | g VS L−1 day−1 | 3 | 3 | 3 | 3 | 3 | 3 | - | - |
| HRT | days | 15 | 15 | 15 | 15 | 15 | 15 | - | - |
| H2 input | L L−1 day−1 | 0.0 | 0.0 | 2.9 | 2.9 | 2.9 | 7.4 | - | - |
| SMPtot | L CH4 g−1 VS | 0.287 | 0.289 | 0.496 | 0.490 | 0.452 | 0.804 | - | - |
| CH4 | % | 50.0 | 50.1 | 93.7 | 90.9 | 75.0 | 76.6 | - | - |
| TAN | M | 0.075 | 0.074 | 0.045 | 0.045 | 0.049 | 0.044 | - | - |
| VFA | M | 0.000 | 0.000 | 0.001 | 0.002 | 0.007 | 0.006 | - | - |
| pH | - | 7.34 | 7.35 | 8.00 | 7.93 | 7.82 | 7.81 | - | - |
| pCO2 | - | 0.474 | 0.473 | 0.040 | 0.046 | 0.071 | 0.077 | - | - |
| a × 108 | - | 9.29 | 9.23 | 22.08 | 23.03 | 19.45 | 18.67 | - | - |
| b × 108 | - | 0.69 | 0.68 | 0.97 | 1.00 | 0.81 | 0.70 | - | - |
| Temp | °C | 37 | 37 | 37 | 37 | 37 | 37 | - | - |
| Difference between experimental and predicted pH based on Eqn A with coefficient a(x) | |||||||||
| a(i) | - | - | 0.00 | 0.32 | 0.35 | 0.29 | 0.27 | 0.28 | 0.995 |
| a(ii) | - | 0.00 | - | 0.33 | 0.35 | 0.29 | 0.28 | 0.28 | 0.996 |
| a(iii) | - | 0.37 | 0.37 | - | 0.02 | 0.05 | 0.07 | 0.24 | 1.000 |
| a(iv) | - | 0.39 | 0.39 | 0.02 | - | 0.07 | 0.09 | 0.25 | 0.998 |
| a(iv) | - | 0.31 | 0.32 | 0.05 | 0.07 | - | 0.02 | 0.20 | 0.998 |
| a(vi) | - | 0.30 | 0.30 | 0.06 | 0.08 | 0.02 | - | 0.19 | 0.998 |
| Difference between experimental and predicted pH based on Equation B with coefficient b(x) | |||||||||
| b(i) | - | - | 0.01 | 0.13 | 0.14 | 0.06 | 0.00 | 0.09 | 0.980 |
| b(ii) | - | 0.01 | - | 0.14 | 0.15 | 0.07 | 0.01 | 0.10 | 0.979 |
| b(iii) | - | 0.14 | 0.15 | - | 0.01 | 0.07 | 0.13 | 0.11 | 0.983 |
| b(iv) | - | 0.16 | 0.17 | 0.01 | - | 0.09 | 0.15 | 0.13 | 0.990 |
| b(iv) | - | 0.06 | 0.07 | 0.07 | 0.08 | - | 0.06 | 0.07 | 0.987 |
| b(vi) | - | 0.00 | 0.01 | 0.13 | 0.14 | 0.06 | - | 0.09 | 0.997 |
| Difference between experimental and predicted pH for Equation A with a(x) and phosphate adjustment | |||||||||
| Period (i) | - | - | 0.01 | 0.05 | 0.07 | 0.06 | 0.01 | 0.05 | 0.993 |
| Period (ii) | - | 0.01 | - | 0.06 | 0.08 | 0.07 | 0.01 | 0.06 | 0.993 |
| Period (iii) | - | 0.06 | 0.07 | - | 0.01 | 0.00 | 0.05 | 0.05 | 0.995 |
| Period (iv) | - | 0.09 | 0.10 | 0.03 | - | 0.02 | 0.07 | 0.07 | 0.996 |
| Period (iv) | - | 0.07 | 0.08 | 0.01 | 0.01 | - | 0.06 | 0.06 | 0.997 |
| Period (vi) | - | 0.01 | 0.02 | 0.04 | 0.06 | 0.05 | - | 0.04 | 0.999 |
| (i) | (ii) | (iii) | (iv) | ||
|---|---|---|---|---|---|
| Before H2 Addition | Baseline Period 1 | Baseline Period 2 | After Recovery | ||
| Day 0–54 | Day 0–24 | Day 25–54 | Day 110–125 | ||
| pH | - | 7.50 ± 0.04 | 7.48 ± 0.04 | 7.50 ± 0.04 | 7.46 ± 0.04 |
| TAN | M | 0.131 ± 0.005 | 0.128 ± 0.004 | 0.134 ± 0.003 | 0.133 ± 0.004 |
| Total VFA | M | 0.008 ± 0.005 | 0.006 ± 0.005 | 0.010 ± 0.004 | 0.006 ± 0.003 |
| TA | g CaCO3 L−1 | 9.38 ± 0.32 | 9.26 ± 0.34 | 9.51 ± 0.22 | 9.37 ± 0.28 |
| PA | g CaCO3 L−1 | 6.33 ± 0.25 | 6.20 ± 0.18 | 6.46 ± 0.22 | 6.40 ± 0.23 |
| IA | g CaCO3 L−1 | 3.05 ± 0.24 | 3.05 ± 0.30 | 3.05 ± 0.17 | 2.97 ± 0.15 |
| TS | %WW | 3.86 ± 0.11 | 3.85 ± 0.11 | 3.88 ± 0.12 | 3.88 ± 0.07 |
| VS | %WW | 2.59 ± 0.09 | 2.59 ± 0.08 | 2.58 ± 0.09 | 2.60 ± 0.06 |
| SMP | L CH4 g−1 VS | 0.358 ± 0.017 | 0.355 ± 0.017 | 0.360 ± 0.017 | 0.322 ± 0.027 |
| pCH4 | - | 0.616 ± 0.008 | 0.617 ± 0.009 | 0.616 ± 0.008 | 0.620 ± 0.009 |
| pCO2 | - | 0.365 ± 0.009 | 0.362 ± 0.010 | 0.367 ± 0.008 | 0.369 ± 0.008 |
| R2 | Slope | Int’cept | RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a × 108 | b × 108 | n | Equation A | Equation B | Equation A | Equation B | Equation A | Equation B | Equation A | Equation B | |
| D1 | 8.29 | 0.962 | 50 | 0.513 | 0.877 | 0.492 | 0.856 | 3.86 | 1.09 | 0.06 | 0.04 |
| D2 | 8.85 | 1.052 | 51 | 0.663 | 0.859 | 0.663 | 1.083 | 2.56 | −0.64 | 0.05 | 0.04 |
| D3 | 8.70 | 1.043 | 51 | 0.774 | 0.937 | 0.915 | 1.000 | 0.68 | 0.02 | 0.08 | 0.04 |
| D4 | 8.45 | 1.023 | 50 | 0.758 | 0.934 | 0.829 | 0.946 | 1.34 | 0.43 | 0.08 | 0.04 |
| D5 | 8.87 | 1.103 | 47 | 0.778 | 0.968 | 0.812 | 0.928 | 1.54 | 0.52 | 0.18 | 0.07 |
| D6 | 9.18 | 1.118 | 50 | 0.917 | 0.962 | 0.895 | 0.972 | 0.82 | 0.17 | 0.08 | 0.06 |
| D7 | 8.96 | 1.134 | 46 | 0.950 | 0.973 | 0.935 | 0.967 | 0.54 | 0.21 | 0.07 | 0.06 |
| D8 | 8.35 | 1.039 | 45 | 0.772 | 0.956 | 0.919 | 1.062 | 0.69 | -0.50 | 0.14 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Heaven, S.; Banks, C.J. Validation of Two Theoretically Derived Equations for Predicting pH in CO2 Biomethanisation. Processes 2023, 11, 113. https://doi.org/10.3390/pr11010113
Zhang Y, Heaven S, Banks CJ. Validation of Two Theoretically Derived Equations for Predicting pH in CO2 Biomethanisation. Processes. 2023; 11(1):113. https://doi.org/10.3390/pr11010113
Chicago/Turabian StyleZhang, Yue, Sonia Heaven, and Charles J. Banks. 2023. "Validation of Two Theoretically Derived Equations for Predicting pH in CO2 Biomethanisation" Processes 11, no. 1: 113. https://doi.org/10.3390/pr11010113
APA StyleZhang, Y., Heaven, S., & Banks, C. J. (2023). Validation of Two Theoretically Derived Equations for Predicting pH in CO2 Biomethanisation. Processes, 11(1), 113. https://doi.org/10.3390/pr11010113