Acoustic Emission Characterization Analysis of Quasi-Static and Fatigue Compression Properties of Aluminum Foam
Abstract
:1. Introduction
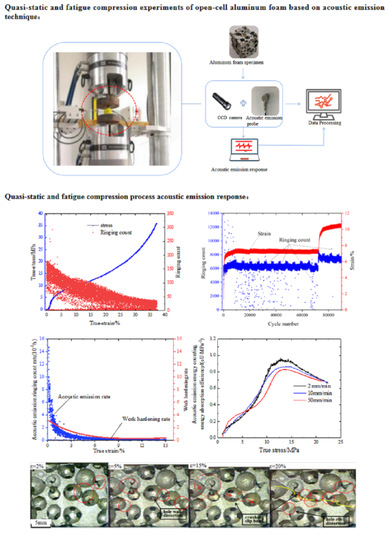
2. Experimental Scheme
3. Experimental Results of Quasi-Static Compression
3.1. Engineering Stress–Strain Curve
3.2. Deformation Characteristics of Surface Images
3.3. AE Response
3.4. AE Energy Count and Energy Absorption Efficiency
3.5. Work Hardening Rate
4. Analysis of Fatigue Test Results
4.1. AE Response
4.2. CCD Surface Images of Fatigue Test
4.3. AE Cumulative Energy of Fatigue Test
5. Conclusions
- (1)
- The AE response during quasi-static compression at different compression rates were consistent with the trend of stress–strain variation. At low compression rates, the AE ring down counts were continuous and serried, and more high energy burst-type AE signals appeared when the cytosol collapsed and fractured in the structure. At high compression rates, the AE ring down counts were continuous and sparse, with larger relative rate of deformation and fewer high energy burst-type AE signals during the collapse of the cytosol.
- (2)
- The work hardening rate curve in the plastic deformation stage of the specimen had the same trend as the AE count rate, and the energy absorption efficiency had the same trend as the AE energy absorption efficiency during quasi-static compression. The engineering strain was around 25%, the energy absorption efficiency reached the maximum, and the energy absorption efficiency of the dense stage decreased.
- (3)
- The responses of AE characteristic parameters were consistent with the fatigue variation pattern of open-cell aluminum foam during fatigue loading with different peak stress ratios. The fatigue failure under high peak stress originated from local collapse due to plastic strain cumulation, and the fatigue failure under low peak stress stemmed from shear deformation of the overall pore wall of the specimen.
- (4)
- During fatigue loading, the deformation of open-cell aluminum foam entered the densification stage after reaching the fatigue life, the AE cumulative count reached its maximum value, the energy cumulative count was large at the low peak stress ratio, and the relative energy was large.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karuppasamy, R.; Barik, D. Production methods of aluminium foam: A brief review. Mater. Today Proc. 2020, 37, 1584–1587. [Google Scholar] [CrossRef]
- Wan, T.; Liu, Y.; Zhou, C.; Chen, X.; Li, Y. Fabrication, properties, and applications of open-cell aluminum foams: A review. J. Mater. Sci. Technol. 2021, 62, 11–24. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, D.; Lee, M.-G.; Lee, J.K. Multiscale Analysis of Open-Cell Aluminum Foam for Impact Energy Absorption. J. Mater. Eng. Perform. 2016, 25, 3977–3984. [Google Scholar] [CrossRef]
- Hajizadeh, M.; Yazdani, M.; Vesali, S.; Khodarahmi, H.; Mostofi, T.M. An experimental investigation into the quasi-static compression behavior of open-cell aluminum foams focusing on controlling the space holder particle size. J. Manuf. Process. 2021, 70, 193–204. [Google Scholar] [CrossRef]
- Jigh, B.H.G.; Toudeshky, H.H.; Farsi, M.A. Experimental and multi-scale analyses of open-celled aluminum foam with hole under compressive quasi-static loading. J. Alloys Compd. 2017, 695, 133–141. [Google Scholar] [CrossRef]
- Hangai, Y.; Ando, M.; Ohashi, M.; Amagai, K.; Suzuki, R.; Matsubara, M.; Yoshikawa, N. Compressive properties of two-layered aluminum foams with closed-cell and open-cell structures. Mater. Today Commun. 2020, 24, 101249. [Google Scholar] [CrossRef]
- Shunmugasamy, V.C.; Mansoor, B. Compressive behavior of a rolled open-cell aluminum foam. Mater. Sci. Eng. A 2018, 715, 281–294. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Li, X.; Lu, C.; Wang, Z.; Wang, W. Energy Absorption Performance of Open-Cell Aluminum Foam and Its Application in Landing Buffer System. J. Mater. Eng. Perform. 2021, 30, 6132–6145. [Google Scholar] [CrossRef]
- Sharma, V.; Grujovic, N.; Zivic, F.; Slavkovic, V. Influence of Porosity on the Mechanical Behavior during Uniaxial Compressive Testing on Voronoi-Based Open-Cell Aluminium Foam. Materials 2019, 12, 1041. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.-Q.; Wang, Z.-H.; Ma, H.-W.; Zhao, L.-M.; Yang, G.-T. Effects of heat treatment on dynamic compressive properties and energy absorption characteristics of open-cell aluminum alloy foams. Trans. Nonferrous Met. Soc. China 2006, 16, 159–163. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Z.; Zhao, L.M. Advances in studies of the mechanical performance of cellular metals and related sandwich structures. Mech. Eng. 2015, 37, 1–24. (In Chinese) [Google Scholar]
- Lu, T.J.; Song, J.M. Characterization of close-celled cellular aluminum alloys. J. Mater. Sci. 2001, 36, 2773–2786. [Google Scholar] [CrossRef]
- Olurin, O.B.; Fleck, N.A.; Ashby, M.F. Deformation and fracture of aluminium foams. Mater. Sci. Eng. A 2000, 291, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Tan, P.J.; Harrigan, J.J.; Reid, S.R. Inertia effects in uniaxial dynamic compression of a closed cell aluminium alloy foam. Mater. Sci. Technol. MST A Publ. Inst. Met. 2002, 18, 480–488. [Google Scholar] [CrossRef]
- Miltz, J.; Gruenbaum, G. Evaluation of cushioning properties of plastic foams from compressive measurements. Polym. Eng. Sci. 1981, 21, 1010–1014. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Hao, H.; Liu, Z.; Yang, Y. Basalt scale-reinforced aluminum foam under static and dynamic loads. Compos. Struct. 2018, 203, 599–613. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, J.; Li, C.B.; Tang, T.; Ouyang, H. Study on acoustic emission characteristics of quasi-static compression for aluminum foam. Suxing Gongcheng Xuebao/J. Plast. Eng. 2018, 25, 189–194. (In Chinese) [Google Scholar]
- Liu, D.Z.; Cheng, X.; Liu, H.; Shen, H.T.; Hua, Z.S.; He, S.W. Improved energy absorption capacity of closed-cell aluminum foams by electroplating. Surf. Eng. 2022, 38, 166–173. [Google Scholar]
- Wang, B.; Wu, B.Y.; Zhou, X.W.; Zhang, W.C. Quasi-static compression test and energy absorption characteristics of closed-cell aluminum foam. J. Foshan Univ. (Nat. Sci. Ed.) 2022, 2, 40. (In Chinese) [Google Scholar]
- Zhao, M.; Fan, X.; Wang, T. Fatigue damage of closed-cell aluminum alloy foam: Modeling and mechanisms. Int. J. Fatigue 2016, 87, 257–265. [Google Scholar] [CrossRef]
- Fan, X.; Zhao, M.; Wang, T. Experimental investigation of the fatigue crack propagation in a closed-cell aluminum alloy foam. Mater. Sci. Eng. A 2017, 708, 424–431. [Google Scholar] [CrossRef]
- Linul, E.; Şerban, D.A.; Marsavina, L.; Kovacik, J. Low-cycle fatigue behaviour of ductile closed-cell aluminum alloy foams. Fatigue Fract. Eng. Mater. Struct. 2016, 40, 597–604. [Google Scholar] [CrossRef]
- Salimi, H.; Hajizadeh, M.; Kalhori, M.R.; Jalili, S.; Yazdani, M. Low-cycle fatigue assessment of open-cell A332 aluminum alloy foams. Int. J. Fatigue 2022, 159, 106797. [Google Scholar] [CrossRef]
- Jigh, B.H.G.; Hosseini-Toudeshky, H.; Farsi, M.A. Low cycle fatigue analyses of open-celled aluminum foam under compression–compression loading using experimental and microstructure finite element analysis. J. Alloys Compd. 2019, 797, 231–236. [Google Scholar] [CrossRef]
- Yang, X.; Hu, Q.; Du, J.; Song, H.; Zou, T.; Sha, J.; He, C.; Zhao, N. Compression fatigue properties of open-cell aluminum foams fabricated by space-holder method. Int. J. Fatigue 2019, 121, 272–280. [Google Scholar] [CrossRef]
- Zhou, J.; Soboyejo, W.O. Compression–compression fatigue of open cell aluminum foams: Macro-/micro- mechanisms and the effects of heat treatment. Mater. Sci. Eng. A 2004, 369, 23–35. [Google Scholar] [CrossRef]
- Yan, C.; Wang, J.; Song, X. Fatigue behavior and damage mechanism of aluminum foam sandwich with carbon-fiber face-sheets. J. Mech. Sci. Technol. 2020, 34, 1119–1127. [Google Scholar] [CrossRef]
- Ingraham, M.; DeMaria, C.; Issen, K.; Morrison, D. Low cycle fatigue of aluminum foam. Mater. Sci. Eng. A 2009, 504, 150–156. [Google Scholar] [CrossRef]
- Shen, G.T.; Geng, R.S.; Liu, S.F. Parameter analysis of acoustic emission signals. Nondestruct. Test. 2002, 24, 72–77. [Google Scholar]
- Loanapakul, T.; Otsuka, Y.; Mutoh, Y. Fatigue and Acoustic Emission Behavior of Plasma Sprayed HAp Top Coat and HAp/Ti Bond Coat with HAp Top Coat on Commercially Pure Titanium. Key Eng. Mater. 2010, 452–453, 857–860. [Google Scholar] [CrossRef]
- Price, E.D.; Lees, A.W.; Friswell, M.I. Detection of severe sliding and pitting fatigue wear regimes through the use of broadband acoustic emission. Arch. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2005, 219, 85–98. [Google Scholar] [CrossRef]
- Fang, D.; Berkovits, A. Evaluation of fatigue damage accumulation by acoustic emission. Fatigue Fract. Eng. Mater. Struct. 2010, 17, 1057–1067. [Google Scholar] [CrossRef]
- Tanvir, F.; Sattar, T.; Mba, D.; Edwards, G. Identification of fatigue damage evaluation using entropy of acoustic emission waveform. SN Appl. Sci. 2019, 2, 138. [Google Scholar] [CrossRef] [Green Version]
- Marfo, A.; Chen, Z.; Li, J. Acoustic emission analysis of fatigue crack growth in steel structure. Acad. J. 2013, 4, 239–249. [Google Scholar]
- Park, H.; Hong, K.; Kang, J.S.; Um, T.; Knapek, M.; Minárik, P.; Sung, P.; Mathis, Y.E.; Yama-moto, K.; Kim, A.; et al. Acoustic emission analysis of the compressive deformation of iron foams and their biocompatibility study. Mater. Sci. Eng. C. Mater. Biogical Appl. 2019, 97, 367–376. [Google Scholar] [CrossRef]
- Brown, J.; Vendra, L.J.; Rabiei, A. Bending properties of Al-steel and steel-steel composite metal foams. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2010, 41, 2784–2793. [Google Scholar] [CrossRef]
- Jenei, P.; Kádár, C.; Szabó, Á.; Hung, S.M.; Kuo, C.J.; Choe, H.; Gubicza, J. Mechanical behavior of freeze-cast Ti foams with varied porosity. Mater. Sci. Eng. A 2022, 855, 143911. [Google Scholar] [CrossRef]
- Yuan, A.; Hou, J.; Yin, Z. The Force Chain and Acoustic Emission Response Law for the Uniaxial Compression of Rock. Geotech. Geol. Eng. 2020, 38, 4479–4499. [Google Scholar] [CrossRef]
- Guo, J.; Shang, W.; Yuan, J.; Liu, Z. Mechanical Behaviors and Damage Evolution Characteristics of Predamaged Rock under Triaxial Compression Experiment. Adv. Mater. Sci. Eng. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Notched marble plates under tension: Detecting prefailure indicators and pre-dicting entrance to the “critical stage”. Fatigue Fract. Eng. Mater. Struct. 2017, 41, 776–786. [Google Scholar] [CrossRef]
- Du, K.; Liu, M.; Yang, C.; Tao, M.; Feng, F.; Wang, S. Mechanical and Acoustic Emission (AE) Char-acteristics of Rocks under Biaxial Confinements. Appl. Sci. 2021, 11, 769. [Google Scholar] [CrossRef]
- Brothers, A.; Prine, D.; Dunand, D. Acoustic emissions analysis of damage in amorphous and crystalline metal foams. Intermetallics 2007, 14, 857–865. [Google Scholar] [CrossRef]
- Kádár, C.; Chmelĺk, F.; Cieslar, M.; Lendvai, J. Acoustic emission of salt-replicated foams during compres-sion. Scr. Mater. 2008, 59, 987–990. [Google Scholar] [CrossRef]
- BS 10/30203543 DC.BS ISO 13314; Mechanical Testing of Metals. Ductility Testing. Compression Test for Porous and Cellular Metals.2010.11.18. International Organization for Standardization: Geneva, Switzerland, 2011.
- Cluff, D.R.A.; Esmaeili, S. Prediction of the effect of artificial aging heat treatment on the yield strength of an open-cell alu-minum foam. J. Mater. Sci. 2008, 43, 1121–1127. [Google Scholar] [CrossRef]
- Oh, K.H.; Jung, C.; Yang, Y.; Han, K.S. Acoustic Emission Behavior during Fatigue Crack Propagation in 304 Stainless Steel. Key Eng. Mater. 2004, 261–263, 1325–1330. [Google Scholar] [CrossRef]
- Wang, W.; Du, G.; Zeng, Z.; Deng, W.; Song, S. Acoustic emission characteristics of corrosion process of 304 nitrogen controlled stainless steel in acidic NaCl solution. Huagong Xuebao/CIESC J. 2010, 61, 916–922. [Google Scholar]
- Miller, R.K.; Mcintier, P. (Eds.) Nondestructive Testing Hand-Book: 5—Acoustic Emission Testing; ASNT: Columbus, OH, USA, 1987. [Google Scholar]
- Wang, Z.; He, A.; Shi, G.; Mei, G. Temperature Effect on AE Energy Characteristics and Damage Mechanical Behaviors of Granite. Int. J. Géoméch. 2018, 18. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Z.Y.; Li, J.H.; Wang, P.; Wu, X.M. Study on the critical condition and deformation mechanism of dynamic recrystallization of novel lightweight steel based on the work hardening rate. Mater. Guide 2022, 19, 36. (In Chinese) [Google Scholar]
- Chen, B.D.; Guo, F.; Wen, J.; Ma, W.; Cai, H.S.; Liu, L. High temperature plastic deformation constitutive model and rheological behavior prediction of Mg-Zn-Zr-Y alloy. Rare Met. Mater. Eng. 2017, 46, 6. (In Chinese) [Google Scholar]
- Van Der Giessen, E.; Tvergaard, V. Micromechanics of intergranular creep failure under cyclic loading. Acta Mater. 1996, 44, 2697–2710. [Google Scholar] [CrossRef] [Green Version]

















| Si | Cu | Mn | Ni | Cr | Fe | Al |
|---|---|---|---|---|---|---|
| 10~13 | ≤0.3 | ≤0.5 | <0.06 | <0.06 | ≤1 | Residual |
| Resonant frequency | 50~500 kHz, central frequency 150 kHz; |
| Temperature range | −40~ + 80; |
| Gain | 34 dB~50 Ohm, = 10 ; |
| Average sensitivity | 90 dB |
| Power Support | |
| Noise impact | Introduced noise 23 dB per five seconds |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Shi, J.; Chen, X. Acoustic Emission Characterization Analysis of Quasi-Static and Fatigue Compression Properties of Aluminum Foam. Processes 2023, 11, 998. https://doi.org/10.3390/pr11040998
Song Q, Shi J, Chen X. Acoustic Emission Characterization Analysis of Quasi-Static and Fatigue Compression Properties of Aluminum Foam. Processes. 2023; 11(4):998. https://doi.org/10.3390/pr11040998
Chicago/Turabian StyleSong, Qiong, Jian Shi, and Xu Chen. 2023. "Acoustic Emission Characterization Analysis of Quasi-Static and Fatigue Compression Properties of Aluminum Foam" Processes 11, no. 4: 998. https://doi.org/10.3390/pr11040998
APA StyleSong, Q., Shi, J., & Chen, X. (2023). Acoustic Emission Characterization Analysis of Quasi-Static and Fatigue Compression Properties of Aluminum Foam. Processes, 11(4), 998. https://doi.org/10.3390/pr11040998