Indirect Monitoring of Anaerobic Digestion for Cheese Whey Treatment

Abstract

Efficient monitoring is an open problem in the operation of anaerobic digestion processes, due to the lack of accurate, low-cost, and proper sensors for the on-line monitoring of key process variables. This paper presents two approaches for the indirect monitoring of the anaerobic digestion of cheese whey wastewater. First, the observability property is addressed using conventional and nonconventional techniques, including an observability index. Then, two model-based observer techniques, an extended Luenberger observer, a sliding mode observer, and a data-driven technique based on fractal analysis are formulated and discussed. The performance and capabilities of the proposed methodologies are illustrated on a validated model with experimental data of the anaerobic digestion of cheese whey. Experimental pH measurements are used for the data-driven approach based on fractal analysis. The experimental data sets correspond to experimental conditions (pH > 7.5 and temperature (T) = 40 °C) favoring volatile fatty acid (VFA) production (30 g/L) with simultaneously acceptable biogas production (3420 mL). Results also show that the proposed observers were able to predict satisfactory key process variables. On the other hand, the fractal analysis provides reliable qualitative trends of VFA production and chemical oxygen demand (COD) consumption.

1. Introduction

Anaerobic digestion (AD) has been used to treat agro-industrial and dairy wastewaters [1,2]. The selection and design of an anaerobic digester depend on several factors, such as organic loads, biological kinetics, and environmental conditions [3,4]. Moreover, due to the continuous variation of wastewater quantity and composition, the AD operation is not a simple task [1,4]. Furthermore, internal and external factors, as well as complex and synergistic interactions between different groups of microorganisms lead to microbial consortium changes [3].

A proper monitoring of the key AD variables is required for process understanding, process control, diagnosis, and making appropriate decisions [4,5,6]. Key process variables and available conventional measurement methods encountered in the field of bioprocesses, include [4,5,6] chemical oxygen demand (COD), which is used as a proxy measure for carbon bioavailability and to quantify the amount of organics in wastewater. Conventional COD measurement uses dichromate or permanganate titration methods [5,7]. More advanced methods include flow-injection analysis using microwave digestion, thermal oxidation techniques, and spectrophotometry [8,9]. In addition, volatile fatty acids (VFAs) are intermediate products of AD, and are one of the major indicators of organic matter degradation present in wastewater. Available methods for VFA measurement include [5,9,10,11,12] fluorescence spectroscopy, near-infrared (NIR) spectroscopy, titration [10], spectrofluorimetric system [11], and gas chromatography [5,9,12]. Lastly, biogas is one of the end products of AD. The measurement of biogas composition (CH₄, CO₂, O₂, H₂S, N₂, and H₂) is performed in specialized devices, such as gas chromatograph, commercial on-line CH₄/CO₂ sensors, and electrochemical cells [5,6]. The biogas mass flow measurement can be realized with advanced thermal mass meters or ultrasonic flowmeters [5,9]. A common method for the quantification of biogas is liquid displacement [13].

Some drawbacks of these methods include [5,9,14] (i) long processing time delays for off-line measurements; (ii) expensive specialized devices and accessories; and (iii) some require costly, corrosive, and highly toxic reagents. Furthermore, bioprocesses are complex and strongly influenced by several factors. Thus, the AD operation is usually limited to the monitoring of pressure, flow rates, temperature, and pH.

The problem of monitoring unmeasured key bioprocess variables has been addressed using two main categories [5,6]: model-based [15,16] and data-driven approaches [6,17]. Model-based approaches depart from a process model and available measurements, such as state observers. In these approaches, one can distinguish the so-called software sensors, including the basic and extended versions of Kalman filters (KF) and Luenberger observers, asymptotic observers, high gain observers, and the interval observer [18,19,20]. On the other hand, data-driven approaches are based only on on-line measurement signals. These approaches include neural networks, support vector machine techniques [16,17], and fractal analysis [21,22].

A vast amount of literature on applications state observers in mechanical, electrical, chemical, and biochemical systems is available [19,23,24]. The proposed state observers vary in complexity and robustness. Some relevant contributions to the estimation of unmeasured key variables in AD are described in the following. Alcaraz-Gonzalez et al. [25] introduce interval observers to estimate four unmeasured variables in a six-state AD model, based on the measurements of organic substrate and VFA. In Morel et al. [26], an observer-based estimator technique using multi-models was developed and applied in lab-scale AD. The observer uses measurements of COD and VFA, and allows the estimation of state variables and kinetic parameters. Super-twisting observers were applied by Sbarciog et al. [27] on the AD benchmark model introduced by Bernard (the AM2 model). For estimation purposes, the authors consider the measurement of both substrate and the flow rate of biogas. In Didi et al. [28], a nonlinear Luenberger type observer was designed for the state estimation of the AM2 model, using both substrates’ measurements. Rodriguez et al. [29] address the states’ simultaneous estimation and kinetic parameters for the AM2 model. They propose an adaptive exponential observer, exploiting the cascade structure of the model using both model substrates as measurable variables. In Lara-Cisneros et al. [30], a nonlinear observer uses a sigmoid-type output injection for the estimation of the VFAs, using the methane flow rate as measured output. The AM2 model is used as the case study. Chaib Draa et al. [31] design a linear matrix inequality (LMI)-based H∞ discrete-time nonlinear state observer. The proposed state observer provides estimates of all state variables using the measurement of the organic substrate, VFA, and the alkalinity concentration in a six-state model. A super twisting-observer was formulated and applied in a two-state AD model by Lara-Cisneros and Dochain [32] to estimate VFA using the methane gas flow as the measured variable. Continuous discrete observers for exogenous input and unknown input based on the extended KF were formulated by Dewasme et al. [33]. The proposed observer’s performance, using as the measured output the flow rate of methane, was tested on a four-state AD model and a pilot-plant AD. Duan and Kravaris [34] exploit the two-time scale of a class of nonlinear systems to propose a nonlinear observer design methodology based on Luenberger observers. A four-state AD model is considered as a case study, and the measured output is the total biomass concentration and the VFA.

The property of observability is a prerequisite for the estimation of non-measurable states through state observers. Various methodologies can be applied to study the observability property with different degrees of complexity [18,19,35]. The observability analysis for linear systems is well established, and includes Kalman’s rank condition, the Gramian of observability, and the Popov–Belevith–Hautus (PBH) criteria [36]. On the other hand, the observability for nonlinear systems is not easy to establish, and is still an open research topic [18,35,37]. Two approaches to address the observability analysis for nonlinear systems are an equivalent Kalmans’ rank condition, using Lie derivatives, and incidence diagrams to establish connections between states and system outputs [35,37,38]. In the case of anaerobic digestion, few papers have addressed the observability properties. Observability analysis based on the rank condition using Lie derivatives was studied by Didi et al. [28] and Rodriguez et al. [29]. Algebraic observability was considered by Lara-Cisneros et al. [30] and Lara-Cisneros and Dochain [32]. In other cases, the observability analysis has been restricted to the classical Kalman´s rank conditions from a local linear approximation of the non-linear model of the process at an equilibrium point [19,34]. It is also noted that due to parameter variations, the process may gradually become unobservable. Moreover, some operating regions in phase space are less observable than others. The concept of observability index was introduced to quantify the degree of observability [35]. Several approaches have been proposed for the observability index. Most of them are based on the observability matrix’s singular values using the corresponding condition number [35,37,38]. A set theoretical approach considering uncertain measurements aimed to control applications was introduced by Lopez et al. [39]. Nahar et al. [40] use an observability index that relates the spatial relationships among all the rows of the observability matrix with the degree of observability.

Data-driven techniques, such as artificial neural networks (ANNs) and support vector machine techniques, allow the estimation of unmeasured key process variables using available measurements that are seemingly unrelated [5,17,19]. ANNs have been applied in AD to estimate removal efficiencies and CO₂ and biogas productions [41,42,43]. In Kazemi et al. [44], different data-driven methods were proposed and evaluated, including ANN and support vector machines, for estimating VFAs using synthetic data from the wastewater treatment Benchmark Simulation Model No. 2. Some limitations of these techniques include the long-term or historic multi-variable measurements, the training step, and the model architecture selection.

In the last few years, fractal analysis has been introduced as an effective diagnostic tool in studying biological fluctuations with efficient handling noise, as well as robustness for unveiling correlations between variables [45,46,47]. Indeed, fractal analysis can reveal the following [21,22,45]: (i) characteristic time scales; (ii) stochastic, persistence, and anti-persistence behaviors; and (iii) dynamic changes of fractal parameters. 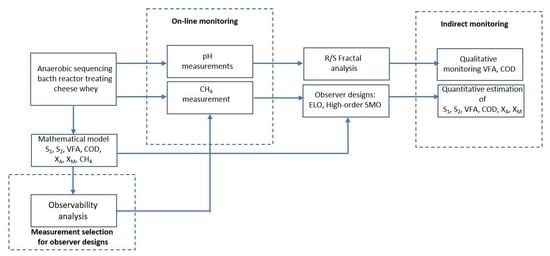In AD, fractal analysis of pH fluctuations has allowed inferring correlations between fractal parameters and key physical parameters (i.e., COD, VFA, and biogas production) [21,22,47].

The objective of this paper is to assess the performance of two model-based estimator approaches, an extended Luenberger observer, and a high-order sliding mode observer [15,19], as well as one data-driven approach based on fractal analysis [21,22,47] for the AD of cheese whey wastewater. Because of their physicochemical characteristics and an elevated amount of organic matter, cheese whey effluents pose severe environmental hazards [48]. The AD of cheese allows potential pollution reduction with simultaneous energy production [49].

The main contributions of this paper are two-fold: (i) it extends the applicability of two indirect monitoring techniques to the AD of cheese whey wastewater using experimental data, and (ii) it presents an in in-depth observability analysis considering conventional and non-conventional methods. Thus, by this contribution, a systematic and practical methodology to address the indirect monitoring of AD processes is provided.

2. Materials and Methods

In this section, the main aspects of the applied methods (observability analysis, state observer designs, and the rescaled range fractal analysis) for the indirect monitoring of key process variables of the cheese whey treatment, using different available experimental information, are described. Moreover, for completeness, both the experimental set-up used to obtain the experimental measurements and the validated mathematical model for observability and observer design purposes are briefly described.

2.1. Experimental Set-Up for Cheese Whey Treatment

The experimental tests were carried out using raw cheese whey as substrate, which was obtained as a byproduct in the fresh cheesemaking process from a community dairy located in Coacoatzintla Veracruz, Mexico. The cheese whey did not receive pretreatment. Moreover, to avoid acidification or chemical composition modification, it was stored at 4 °C for no more than 12 h before its use. The sludge used as inoculum was conditioned in a laboratory-scale anaerobic digester fed with raw cheese whey (organic load rate OLR = 3.6 gCOD L⁻¹ d⁻¹) under conditions of 33 °C, pH = 8.0, hydraulic retention time (HRT) = 30 d, and having been operated for 365 days.

Anaerobic treatment of raw cheese whey was carried out in duplicate using a batch reactor with an effective volume of 5.1 L, operated at initial pH = 7.5 and under mesophilic conditions, maintaining the reactor temperature at 40 °C by controlling the circulation of the cooling water. The pH control system was only established to avoid acidification of the system, i.e., when the pH is lower than the initial pH, an NaOH solution was added.

For process monitoring, pH, temperature, and the biogas flow rate were monitored online, and VFAs and COD were monitored offline using standardized analytical techniques. Biogas production was measured on a daily basis by using the volumetric methodology. Biogas composition was measured using a GOW-MAC 580 series gas chromatograph, equipped with an isothermal column oven, and hauling gas of helium and hydrogen. The pH measurements were sampled at 1 data per second for 5 days (432,000 points), with an accuracy of ±0.02, using a National Instrument cRIO-9074 system with a Mettler-Toledo M300 pH/ORP transmitter.

2.2. Mathematical Model for Cheese Whey Treatment

An unstructured dynamical model describing the behavior of the AD of cheese whey was proposed by B-Arrollo et al. [50]. The model parameters were estimated using Levenberg–Marquardt’s method, based on experimental data sets from the above-described experimental set-up. The effects of pH and temperature variations are also considered in the proposed model. Hence, this experimentally validated model has been used as the base model for observability analysis and observer designs described below.

The main model assumptions [50] are (i) four consecutive stages—hydrolysis, acidogenesis, acetogenesis, and methanogenesis; (ii) homogeneous conditions; (iii) that the organic load is lumped into two substrates, S₁ (g/L) and S₂ (g/L), where S₁ lumps the long-chain components (carbohydrates, proteins, and lipids) and S₂ represents simple organic compounds (carbohydrates and amino acids); (iv) the AD biomass is lumped into three species—hydrolytic biomass X_h (g/L), acidogenic bacteria X_A (g/L), and methanogenic biomass X_m (g/L); (v) the acidogenic bacteria X_A consumes S₂ to produce the VFA (A); (vi) the methanogenic biomass X_m produces biogas B; (vii) first-order kinetics is used for the hydrolysis phase; (viii) the kinetics of the acidogenesis step is described with a Monod kinetic; and (ix) the methanogenic growth is described with Haldane kinetics, which considers VFA inhibition. The mathematical model is given by B-Arrollo et al. [50].

$$\frac{d{X}_h}{dt}=K_h{S}_1{X}_h-K_{dh}{X}_h$$

$$\frac{d{S}_1}{dt}=-\frac{K_h{S}_1{X}_h}{Y_{X_h/S_1}}$$

$$\frac{d{X}_A}{dt}=\frac{{\mu }_{amax}{S}_2}{K_{S2}+S_2}I{X}_A-K_{da}{X}_A$$

$$\frac{d{S}_2}{dt}=K_h{S}_1{X}_h{Y}_{S_2/X_h} -\frac{1}{Y_{X_A/S_2}}\frac{{\mu }_{amax}{S}_2}{K_{S2}+S_2}I{X}_A$$

(1)

$$\frac{d{X}_m}{dt}= \frac{{\mu }_{mmax}A}{K_A+A+A^2/K_I}I{X}_m-K_{dm}{X}_m$$

$$\frac{dA}{dt}=Y_{A/X_a}\frac{{\mu }_{amax}{S}_2}{K_{S2}+S_2}I{X}_a-\frac{1}{Y_{X_m/A}}\frac{{\mu }_{mmax}A}{K_A+A+A^2/K_I}I{X}_m$$

$$\frac{dC{H}_4}{dt}=Y_{C{H}_4/X_m} \frac{{\mu }_{mmax}A}{K_A+A+A^2/K_I}I{X}_m$$

where K_h is the hydrolytic constant, and the death constants of the hydrolytic, acidogenic, and methanogenic bacteria are K_dh, K_da, and K_dm, respectively. The production yield coefficients are Y_Xh/S1, Y_S2/Xh, Y_A/Xa, and Y_CH4/Xm. Degradation yield coefficients are Y_Xa/S2 and Y_Xm/A. Maximum growth rates are µ_amax, and µ_mmax for the acidogenesis and methanogenic kinetics, respectively. The kinetic constants are K_S2, K_A, and K_Im. Variable I was introduced into the model to consider the simultaneous effects of pH and temperature on the biomass kinetics. Additional model details are found in B-Arrollo et al. [50].

2.3. Observability Analysis

Observability is a structural system property to identify the possibility of inferring the unmeasured states based on available measurements. In this section, the observability properties using linear and non-linear approaches are briefly described.

2.3.1. Linear Observability Analysis

Linear observability criteria are based on the linearized version of the non-linear model. Thus, consider the classical linear state–space approximation, given by

$$\begin{array}{c}\frac{dx\left(t\right)}{dt}=A\left(t\right)x\left(t\right)+B\left(t\right)u\left(t\right)\\ y\left(t\right)=C\left(t\right)x\left(t\right)+D\left(t\right)u\left(t\right)\end{array}$$

(2)

where A(t) is the matrix of states, B(t) is the matrix of inputs, C(t) is the matrix of outputs, and D(t) is the matrix of measured inputs. If A, B, C, D are constant matrices, model (2) represents the most common linear time-invariant system (LTI) for linear control studies [36].

• Kalman range condition.

The classic observability test, the Kalman range condition [36], states that the LTI system is observable if and only if the following observability matrix O_Kal has a full range,

$$O_{Kal}={\left[C CA C{A}^2\dots \dots .C{A}^{N-1}\right]}^T$$

(3)

Kalman´s range condition is based on the fact that if there are N columns independent of O_Kal, then each state variable can be determined by a linear combination of the output variable y(t) and the time t [36].

2.

Popov–Belevitch–Hautus (PBH) test.

For LTI systems with an accurate knowledge of system parameters, the PBH observability test establishes that an LTI system is observable if and only if [36]

$$rank\left[\begin{array}{c}sI-A\\ C\end{array}\right]=N \forall {\lambda }_i\in A$$

(4)

It can be noted that the test requires evaluating Equation (4) for each eigenvalue of A. It also should be noted that the above observability conditions, i.e., the Kalman rank condition, the PBH test, and the corresponding Gramian test, are equivalent and applicable to the LTI version given by the state–space model (2).

For non-linear observability analysis, consider the following non-linear system,

$$\begin{array}{c}\frac{dx\left(t\right)}{dt}=f\left(x\left(t\right),u\left(t\right)\right)\\ y\left(t\right)=hx\left(t\right)\end{array}$$

(5)

where x(t) is the vector of states of the system, and y(t) is the vector of measurable outputs.

• Rank condition using Lie derivatives.

The observability concept for non-linear systems was extended using differential geometry concepts [35,38]. In this case, observability can be established locally from an observability matrix that is constructed with Lie derivatives or square brackets, given as

$$O_{Lie}={\left[h\left(x\right){ℒ}_{f}h\left(x\right) {ℒ}_f^{2}h\left(x\right)\dots \dots {ℒ}_f^{N-1}h\left(x\right)\right]}^T$$

(6)

A sufficient observability condition for the nonlinear system given by Equation (5) is that the observability matrix O_Lie, given by Equation (6), is of a dimension equal to the dimension of the vector of states N [35]. The observability matrix given by Equation (6) can be considered a generalization for non-linear systems of the observability matrix given by Equation (3) for linear systems. Due to the more considerable computational effort of the Lie derivatives calculation, an observability condition using the simple linear approximation is more common.

2.

Incidence diagrams.

The observability property can be studied by exploiting the structure of the connections between the states, inputs, and outputs of the system, using a graphic representation [35,37]. Liu et al. [35] describe the approach to building an inference diagram based on the system model’s structure. The incidence diagram is constructed considering the following points [35]:

• A link is drawn, x_i → x_j, if x_j appears in the differential equation of x_i. This implies that one can collect information from x_j by monitoring x_i as a function of time;
• The inference diagram is broken down into sets of firmly connected maximum components (SCCs), which are select graphs that directly link to each node of another sub-graph. Usually, they are enclosed in dotted circles;
• At least one node is selected from each root of the SCCs, which do not have input axes, to ensure system observability.

Thus, the incidence diagram approach provides a practical observability analysis based on the nonlinear systems.

2.3.2. Observability Index

The observability index was introduced to provide information on the singularity of the observability matrix [37]. Indeed, when the observability matrix is near the singularity, the observability properties are lost, leading to problems in the estimation of unmeasured states or in observer-based control schemes. This paper considers the observability index applied by Nahar et al. [40] to an agro-hydrological system, which relates the spatial relationships among all the rows of the observability matrix with the degree of observability. Hence, the degree of observability is quantified with the smallest eigenvalue of the product ø^Tø, where ø denotes the normalized observability matrix at the sampling time k, which is written as

$$O\left(k\right)={\left[C\left(k\right) C\left(k\right)A\left(k\right) C\left(k\right)A{\left(k\right)}^2\dots \dots .C\left(k\right)A{\left(k\right)}^{N-1}\right]}^T$$

(7)

The normalized element at the j-th row and the i-th column in matrix ø is computed as follows [40]:

$${ø}_i^j=\frac{O_i^j}{\sqrt{\left({\sum }_{i=1}^N{\left|O_i^j\right|}^2\right)}}$$

(8)

where O^j are the rows of observability matrix O. The degree of observability is then given as [40]

$$degø={\lambda }_{min}$$

(9)

where λ_min is the minimum among all the eigenvalues λ_i (i = 1, …, N). The ratio of eigenvalues gives the relative measure of system observability [40]:

$$ø=\frac{{\lambda }_{max}}{{\lambda }_{min}}$$

(10)

where λ_max is the maximum eigenvalue of ø^Tø. A value of Ɵ closer to one is associated with a highly observable system. On the other hand, larger values of Ɵ correspond to poorly observable conditions [40].

2.4. Observer Designs

The following dynamic model gives the general structure of a nonlinear observer for the nonlinear system (5):

$$\frac{d\widehat{x}}{dt}=f\left(\widehat{x}\left(t\right),u\left(t\right)\right)+\phi \left(e_e\left(t\right)\right)$$

(11)

with

$$e_e=y\left(t\right)-\widehat{y}\left(t\right)$$

(12)

where $\widehat{x}\left(t\right)$ is the vector of the estimated states and $\widehat{y}\left(t\right)$ is the estimation of the measured states. Thus, the observer design structure consists of a copy of the process model, plus a corrective term $\phi \left(e_e\left(t\right)\right)$ driven by the measured signal y(t) [15,19,23]. The observer problem´s design is to devise the form of function φ, such that $\Vert x\left(t\right)-\widehat{x}\left(t\right)\Vert$ → 0, either asymptotically (t → ∞) or in finite time (t → t_f).

2.4.1. Extended Luenberger Observer

The structure of the extended Luenberger observer (ELO) is obtained with the correction term, selected as [15,19]

$$\phi \left(e_e\left(t\right)\right)=L\left(y\left(t\right)-\widehat{y}\left(t\right)\right)$$

(13)

L is the gain observer matrix, which can be calculated to guarantee the desired convergence rate and its stability [19,23]. Nonetheless, the computing of L requires model linearization, which is valid only around a given linearization point.

2.4.2. Sliding Mode Observers

Sliding mode observers (SMOs) belong to the class of high-gain observer (HGO) designs, with a convergence rate higher than the ELO [19,27]. SMOs are a family of observer designs based on the convergence properties of a switching action driven by a sign function. Indeed, in SMOs, a discontinuous action is used to reach the so-called sliding surface for which the state estimation error is zero. Thus, roughly speaking, in SMOs the correction term is endowed with a discontinuous switched signal.

High-order SMOs have been proposed to provide smooth estimation in finite time [51,52]. In this paper, a high-order SMO is proposed to estimate the model states from the only experimental measurement of CH₄. The correction term is then given as [51,52]

$$\phi \left(e_e\left(t\right)\right)=Ksign\left(y\left(t\right)-\widehat{y}\left(t\right)\right)\Vert y\left(t\right)-\widehat{y}\left(t\right){\Vert }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}$$

(14)

where K is an observer design parameter and p is an odd number.

2.5. Fractal Analysis

Data-driven techniques offer the possibility to use data sets of available measurements, such as temperature, pH, conductivity, etc., and establish a map to some of the key process variables [17,41,42,43,44]. Fractal analysis is a simple, data-driven technique proven quite useful and effective to infer unmeasurable variables in many process applications [21,53,54]. Several methodologies are available in the literature for fractal analysis. However, rescaled range (R/S) has been widely applied for time-series analysis obtained from physical, chemical, and biological processes, due to its simplicity and easy implementation [55]. The R/S statistical measures the range of the partial sums’ deviations in a time series about its average, rescaled by the series standard deviation. Consider a time series Z_N = (z_i) of length N, and the subsequence X_NS = (x_i) of length N_S, where N_S < N. The R/S statistic for X_NS is calculated as [55]

$${\left(\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$S$}\right.\right)}_S=\frac{1}{{\sigma }_S\left(N_S\right)}\left({}_{1\le i\le M}{}^{max}\sum _{k=1}^i(x_k-{\overline{x}}_{NS})\right)$$

(15)

where ${\overline{x}}_{Ns}$ is the subsequent mean, ${\overline{x}}_{Ns}=\frac{1}{N_S}{\displaystyle \sum _{i=1}^{Ns}{x}_i}$, and ${\sigma }_S(N_S)$ is the sample standard deviation ${\sigma }_S(N_S)=\sqrt{\frac{1}{N_S}{\displaystyle \sum _{k=1}^{N_S}{(x_k-{\overline{x}}_{Ns})}^2}}$. The R/S statistic can be described with a power law, ${(R/S)}_S=a{N}_S^H$, where a is a constant and H is the Hurst exponent. In the pox diagram, obtained with a log–log plot of (R/S) as a function of $N_S\in (N_{S,\min },N_{S,\max }),$ gives a straight line with slope H. For independent series data (e.g., white noise process), H = 0.5. If H > 0.5, the time series is persistent, indicating the presence of long-term autocorrelations. Finally, if H < 0.5, the series data displays anti-persistent autocorrelations. Dynamical changes of the Hurst exponent are obtained considering a moving window of m points.

3. Results and Discussion

In this section, we discuss the application and limitations of the above-described methods for the indirect monitoring of key process variables in cheese whey wastewater treatment. For numerical simulations and computational analysis, the following numerical parameter values were considered [50]: K_h = 100, K_dh = 100, K_da = 100, K_dm = 100, Y_Xh/S1 = 100, Y_S2/Xh = 100, Y_A/Xa = 100, Y_CH4/Xm = 100, Y_Xa/S2 = 100, Y_Xm/A = 100, µ_amax = 100, µ_m = 100, K_S2 = 100, K_A = 100, and K_Im = 100. Initial conditions were set as [S₁, S₂, X_h, X_A, X_m, A, CH₄] = [20.3342, 36.1908, 0.9969, 1.047, 0.3287, 94.5439, 0].

3.1. Experimental Profiles

Figure 1 shows the experimental profiles of COD, VFA, and biogas production, during 120 hours of operation of the anaerobic sequencing batch reactor (AnSBR) treating the cheese whey, and nominal conditions of pH = 7.5 and temperature (T) = 40 °C [50]. Experimental results present a percentage of COD removal of 35%, a VFA generation of 30 g/L, and biogas production of 3420 mL. The pH was maintained above the base value of pH = 7.5 to avoid the system’s acidification with a simple on/off control scheme. Despite the fact that pH fluctuations are typically assumed to be non-correlated noise, providing information related to process acidification, such a pH fluctuations, reflects essential aspects of the digester metabolic status.

3.2. Observability Analysis

Following the graphical approach method by Liu et al. [35], Figure 2 shows the constructed inference diagrams for cheese whey AD. It is noted from the incidence diagram that the CH₄ state is the only root SCC, i.e., one that has no incoming edges. Thus, the CH₄ measurement, which is available using different conventional techniques, is necessary to ensure the whole system’s observability.

Since incidence diagrams provide necessary conditions for observing the non-linear system’s states, the Kalman rank condition and the observability matrix’s rank condition based on Lie derivatives were computed. The structures of both the standard observability matrix and observability matrix using Lie derivatives are identical and given as

$$O=\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 1\\ 0& 0& J_{23}& J_{24}& J_{25}& J_{26}& 0\\ J_{31}& J_{32}& J_{33}& J_{34}& J_{35}& J_{36}& 0\\ J_{41}& J_{42}& J_{43}& J_{44}& J_{45}& J_{46}& 0\\ J_{51}& J_{52}& J_{53}& J_{54}& J_{55}& J_{56}& 0\\ J_{61}& J_{62}& J_{63}& J_{64}& J_{65}& J_{66}& 0\\ J_{71}& J_{72}& J_{73}& J_{74}& J_{75}& J_{76}& 0\end{array}\right]$$

(16)

where J_ij denotes the corresponding non-vanish element in the i-th row and j-th column of the corresponding observability matrix. Thus, in both cases, the full rank condition is satisfied with the measurement of CH₄.

The observability index’s behavior, considering the measurement of CH₄, along the trajectory of model (1) for 120 h, is shown in Figure 3. It is noted that the observability index’s lower values are obtained at the beginning of the dynamic simulation until 45 h. In 45–100 h, considerable fluctuations are shown, indicating poor full-state observability properties using only the measurement of CH₄. For comparison purposes, the observability index using the simultaneous measurement of CH₄ and VFAs is also presented in Figure 3. Interestingly, after a slight fluctuation at the time interval of 45–60 h, observability properties are improved, which can reflect that the production of VFAs and thus better reflect the status of the AD. In fact, at t = 45 h, the maximum production of S₂ is achieved; after that, fast consumption of this substrate from the acidogenic bacteria is observed.

3.3. Observer Designs

Based on previous observability analysis, for observer designs, the measured variable is selected as the CH₄ concentration. It should be noted that several observer designs applied to AD units consider as available measurements the VFA and COD concentrations [25,27,28,29], which is only possible using costly measurement devices, limiting its practical applicability. On the other hand, other observer designs, utilizing the methane gas flow as a measurement variable [30,31,33], have been applied to reduced AD models.

Figure 4 shows the performance of both the ELO and high-order SMOHOSMO observer designs. The ELO gain matrix is determined based on the LMI methodology [56]. The gains of the sliding mode observer are selected by trial and error. Both observers are driven by a simple interpolation of available experimental measurement of CH₄ (13 points at different sampling times) and its corresponding estimated value from the observers.

A similar behavior of each observer designs for the estimation of substrates S₁ and S₂ can be noted from Figure 4. The most important differences between estimated states and the experimental data are observed before the substrates’ depletion.

The observer performance was evaluated using the normalized mean squared error (NMSE), given as

$$NMSE=\frac{1}{N}{\displaystyle \sum }_{i=1}\frac{{\left(P_i-M_i\right)}^2}{\overline{P}\ast \overline{M}}, \overline{P}=\frac{1}{N}{\displaystyle \sum }_i{P}_i, \overline{M}=\frac{1}{N}{\displaystyle \sum }_i{M}_i$$

where P_i and M_i are experimental and estimated values, respectively. Results are shown in

Table 1. Performance indexes (normalized mean squared error (NMSE)) for the ELO and high-order SMO.

NMSE	ELO	High-Order SMO
CH4	0.01006	0.0079
VFA (A)	0.0269	0.0304
S1	0.0601	0.0601
S2	0.01502	0.0153

.

The analysis of the results obtained shows a similar performance of both observer designs. However, the ELO was slightly superior to the performance of the high-order SMO.

3.4. Fractal Analysis

R/S analysis was applied to the experimental pH time series collected in the fermentation of raw whey. Figure 5 shows the R/S statistic as a function of the scale s, calculated using the complete pH time series (global analysis), and considering samples from the 6 h pH time series (local analysis). The global analysis shows three different Hurst exponent values corresponding to regions A, B, and C, suggesting that the R/S analysis can identify three characteristic phenomena in the anaerobic treatment of raw cheese whey. Sanchez-Garcia et al. [47] indicate that each region can be related to a stage of the AD process, i.e., region A is associated with hydrolysis, region B to acidogenesis, and region C to methanogenesis. The local R/S analysis shows that the three regions are conserved in the analyzed samples. However, the slopes (i.e., Hurst exponent values) exhibit dynamic variations as the process is performed, which suggests that the calculated Hurst exponents could be correlated to dynamic changes in the process stages.

To analyze such dynamic Hurst exponent changes, a 6 h window was used, moving through the entire time series in 1 h increments, which allowed the calculation of the Hurst exponent values as a function of scale and time. According to Mendez-Acosta et al. [21], the average of each region can be used as an index of the dynamic behavior of COD consumption or VFA production. Figure 6 shows the averages of regions A and C compared with COD consumption and total VFA production, respectively. Hurst exponents and experimental data exhibit the same trend, corroborating that R/S analysis is a statistical technique that allows identification of the stages of whey fermentation and indirect monitoring of the key process parameters. Thus, the results presented in this section extend the results found by Sanchez-Garcia et al. [47] under different operation conditions, including a wider pH variability. Moreover, the same experimental conditions and data are used for the observability analysis, as well as the observer’s evaluations. It should be noted that it was not possible to determine correlations for the biogas production, such as those obtained by Sanchez-García et al. [47], since the process operation conditions in this study favor the VFA production. Conditions established in Sanchez- Garcia et al., [47] were established to favor biogas production.

For diagnostic purposes, Morel et al. [26] use a knowledge-based system based on measurements of biogas composition and pH, which allow the prediction of different process conditions (methanogenic, organic overload, and acidogenic) in an AD unit. Thus, the fractal analysis offers an alternative to process diagnoses based only on the measurement of pH.

4. Conclusions

Anaerobic digestion processes are broadly used for treating agro-industrial and dairy wastewaters. Effective monitoring and diagnostics technologies are mandatory to improve AD performance. In this paper, the indirect monitoring of key process variables of the AD of cheese whey was addressed using both model-based and data-driven approaches. Experimental data from an anaerobic sequencing batch reactor operated at pH > 7.5 and T = 40 °C, favoring that VFA production is used to validate and evaluate the performance of both approaches. Moreover, an in-depth observability analysis was performed to identify the most convenient measurement process variable that guarantees process observability. It can be established that the observability analysis by differential geometry, together with the inference diagram, are the tools that provide a complete observability assessment for the AD of cheese whey. Two model-based monitoring approaches were applied, an extended Luenberger observer and a high-order sliding mode observer, to monitor substrate consumption and VFA production in the AD of cheese whey, based on the single measurement of CH₄. The performance of proposed observers was quantified with the NMSE. The extended Luenberger observer presents a slightly better global performance for the estimation of key process variables. A data-driven approach based on fractal analysis of the single measurement of pH of the AD of cheese whey was also presented. Dynamical changes of fractal parameters can be used for the qualitative monitoring of key bioprocess variables. Since fractal analysis allows qualitative monitoring, its application is limited for control design purposes. However, due to its fast and low computational demand, it can be useful for diagnostics purposes of the AD operation, enabling fast and simple detection of process failures. Although the indirect monitoring study is restricted to the AD of cheese whey, the general ideas of the observability analysis, observer designs, and fractal analysis presented here present a systematic framework for the reliable monitoring of a broad class of AD processes.