Next Article in Journal
Solvent and Substituent Effects on the Phosphine + CO2 Reaction
Previous Article in Journal
Synthesis and Characterization of the New Dicyanamide LiCs2[N(CN)2]3
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 6
Issue 4
10.3390/inorganics6040109
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Synthesis and Structural Characterization of Ba7Li11Bi10 and AE4(Li,Tr)7Pn6 (AE = Sr, Ba, Eu; Tr = Ga, In; Pn = Sb, Bi)

by
Dickson O. Ojwang
and
Svilen Bobev
*
Department of Chemistry and Biochemistry, University of Delaware, Newark, DE 19716, USA
*
Author to whom correspondence should be addressed.
Inorganics 2018, 6(4), 109; https://doi.org/10.3390/inorganics6040109
Submission received: 12 September 2018 / Revised: 27 September 2018 / Accepted: 28 September 2018 / Published: 6 October 2018
(This article belongs to the Section Inorganic Solid-State Chemistry)
Browse Figures
Versions Notes

Abstract

:
Reported are the synthesis and crystal structure of Ba7Li11Bi10, a new ternary compound crystallizing in its own type with the monoclinic space group C2/m (a = 18.407(3) Å, b = 5.0258(9) Å, and c = 18.353(3) Å; β = 104.43(1)°; Pearson symbol mS56), and those of the structurally related quaternary phases Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6 (crystallizing in the Eu4Li7Bi6 structure type with the same monoclinic space group C2/m (a = 18.4045(13)–17.642(4) Å, b = 5.012(4)–4.8297(10) Å, and c = 13.2792(10)–12.850(3) Å, β = 126.80(1)–125.85(1)°; Pearson symbol mS34). All studied compounds are identified among the products of the high-temperature reactions of the corresponding elements. Both types of crystal structures are based on corner- and edge-linked Li-centered Sb4 (or Bi4) tetrahedra, Sb6 (or Bi6) octahedra, and Sb2 or Bi2 dumbbells. Given the similarities between the two structures, it might be proposed that they represent the simplest members of a potentially large homologous series described with the general formulae (BaLi3Sb2)n(Ba3Li4Sb4)m or (BaLi3Bi2)n(Ba3Li4Bi4)m, where the more complicated “7-11-10” phase is the member with n = 2 and m = 1, while the “4-7-6” one is the intergrowth of the two components in an equal ratio. The computed electronic band structures of Ba7Li11Bi10 and idealized Ba4Li7Bi6 (a model for Ba4(Li1−xInx)7Bi6) are also discussed.

Graphical Abstract

1. Introduction

Zintl phases represent a diverse class of compounds with complicated crystal and electronic structures. They display a wide variety of traits and they are potentially promising candidates for electronic, magnetic, superconductive, semiconductive, and thermoelectric materials, and therefore they have attracted much attention over the years [1,2,3]. To such, a host of Zintl compounds, e.g., Eu5In2Sb6, Ca5Ga2As6, Sr3AlSb3, Ca5In2Sb6, and Ca5Al2Sb6 etc., have been explored as thermoelectric materials because of their low lattice thermal conductivities [4,5,6,7,8]. For over a decade, our group has been working on the synthesis, structural chemistry, and properties of Zintl phases and intermetallic compounds comprising alkali, alkaline-earth, or rare-earth metals, and the pnictogens (Pn), e.g., Na11Ca2Al3Sb8, Ba4Li2Cd3Pn6, AE3Al2Pn4, and AE7Ga2Sb6 (Pn = P, As, Sb; AE = Ca, Sr, Ba, Eu) [9,10,11,12]. Recent investigations of the RELi3Pn2, AELiPn, and AE3Li4Pn4 (RE = rare-earth metals; AE = Ca, Sr, Ba, Yb; Pn = As, Sb, Bi) series led to the discovery of the unique monoclinic compound Eu4Li7Bi6 (space group C2/m with own structure type) [13]. Studying its structure, one might conclude that applying the Zintl–Klemm formalism to rationalize it; namely, the electron counting scheme (Eu2+)4(Li+)7([Bi2]4−)(Bi3−)4(h+) (the symbol h+ denotes an electron hole), leaves some open questions. First, what is the root cause for the apparent electron-deficiency in this case? Second, could that lack of charge-balance according to the Zintl–Klemm concept be an artifact of the over-simplified way that the complex bonding is treated? In an earlier publication [13], we tried to address these issues by carrying out electronic structure calculations, which confirmed the perceived electron deficiency. In light of the very limited experimental data on this structure, it was proposed that Eu4Li7Bi6 could be an example where Eu has a mixed oxidation state, or, it could be an impurity-stabilized phase.
This unexpected finding encouraged us to study analogous compounds by exploring the series AE4Li7Pn6 (AE = Sr, Ba, Eu; Pn = Sb, Bi). The idea was that if Sr and Ba, alkaline-earth metals that have only one stable oxidation state, 2+, can form the same structure, the uncertainty surrounding the state of Eu would be lifted, and it would be established that the electron-deficiency is an inherent feature of the structure. At the same time, experiments aimed at making AE4(Li1−xGax)7Pn6 and AE4(Li1−xInx)7Pn6, isostructural to AE4Li7Pn6 (but not isoelectronic) were carried out with the idea of verifying whether Li atoms can be partially substituted by small amounts of Ga or In, thereby tuning the number of valence electrons to the “proper” level. Ga and In were chosen because of the demonstrated tendency of these elements to mix in the crystal structures of related alkaline-earth metal lithium germanides and stannides, e.g., AELi1−xInxGe2, RE4Li4−xSn4+x, and Li9−xEuSn6+x [14,15,16].
Herein we describe the results of these studies, focusing on the crystal and electronic structures of the compounds Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6, all of which show partial substitution of Li by Ga or In at a level of x ≈ 0.06–0.08, i.e., near the electron-precise Zintl phase-like composition. In addition, the exploratory work in these systems allowed for the identification of a completely new ternary bismuthide, Ba7Li11Bi10, which crystallizes with its own monoclinic structure type, C2/m. The electronic structure calculations of the idealized Ba4Li7Bi6 (a model for the actual Ba4(Li1−xInx)7Bi6) and Ba7Li11Bi10 compounds are also presented.

2. Results and Discussion

2.1. Crystal Structure and Bonding in Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6

All the compounds of the “4-7-6” variety crystallize in the monoclinic space group C2/m with their own structure type [13]. There are a total of 34 atoms in the unit cell and two formula units, thus, the Pearson symbol of this structure is mS34.
A ternary compound with this structure was reported by us in 2014, namely Eu4Li7Bi6 [13]. At that time, the structure was considered unique, although we noted the existence of the phase known as Ba8Li13GaSb12, reported eight years earlier [17]. Because the latter was worked out in non-standard coordinate settings (the published Wyckoff sequence of the structure is i8 d) [17], ICSD references it as isotypic to the Ce4Mg7Ge6-type structure [18]. Our analysis from 2014 of the bonding in Eu4Li7Bi6 [13] and Ce4Mg7Ge6 [18] indicated that although both have the same C2/m space group and same number of atoms in the unit cell, the structures are sufficiently different and should not be considered isotypic. This conjecture is also supported by the standardized version of the coordinates, which shows that Eu4Li7Bi6 and its herein presented analogs have an i8 c Wyckoff sequence. Furthermore, the refined structure of Ba4(Li1−xGax)7Sb6 (x ≈ 0.08, i.e., Ba4(Li0.92Ga0.08)7Sb6 = Ba4Li~6.4Ga~0.6Sb6) shows that the previously reported Ba8Li13GaSb12 (=Ba4Li6.5Ga0.5Sb6) has the same structure as all other members of the “4-7-6” family of pnictides (Table 1, Table 2 and Table 3), and that the structures of the ternary rare-earth metal–magnesium germanides belonging to the Ce4Mg7Ge6 structure type are related, but not identical.
Crystallographic data for several crystals from each of the Ba4(Li1−xInx)7Sb6 and Ba4(Li1−xInx)7Bi6 structures are listed in Table 2. The analogous information from two Eu4(Li1−xInx)7Bi6 crystals is given in Table 3. In all cases, the refined parameters included the scaling factors, atomic coordinates, displacement parameters, and where applicable—the extinction coefficient and occupancy factors. Relevant interatomic distances in the Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6 structures are displayed in Table 4. Points of specific interest will be discussed in detail later, here, but we just mention that all of the AE–Pn, Pn–Pn, and Li–Pn distances are distributed between 3.6487(6)–3.3394(6) Å, 3.0589(9)–2.8472(10) Å, and 3.4407(4)–2.799(9) Å, respectively. These metrics are consistent with those reported for CaLiSb, BaLiSb, Ba3Li4Sb4, SrLiBi, Ba3Li4Bi4, and Eu4Li7Bi6 [13,19,20,21,22,23].
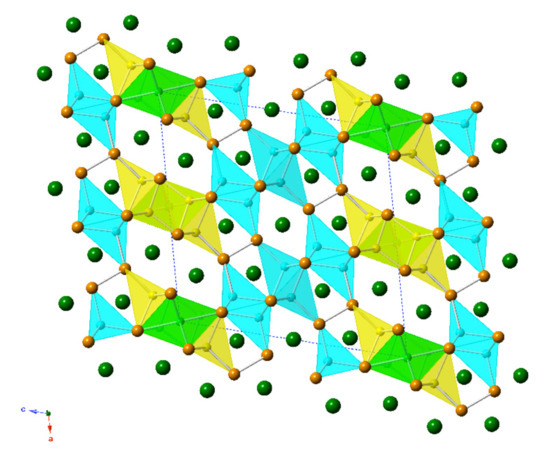
The overall structure is schematically shown in Figure 1. As seen in the structural representation, there are different coordination polyhedra. Li1, Li2, and Li3 atoms are all tetrahedrally coordinated by Sb, while Li4 is octahedrally coordinated. The polyhedra interact through edge and corner sharing. Naturally, because of the arrangement of these fused polyhedra, some relatively short Li–Li contacts arise (Li1–Li3 3.05(1) Å, Li1–Li4 2.98(3) Å). However, considering the Pauling single-bonded radius, rLi = 1.225 Å [24], such distances are not indicative of strong bonding interactions. Pn1 atoms form [Pn2]4− dimers (isoelectronic with the I2 molecule), while Pn2 and Pn3 atoms exist as isolated Pn3− ions. In the tetrahedra where Li is mixed and occupied with Ga or In, the distances to the closest neighbors vary from 2.867(5) to 3.071(2) Å. Note also that the Sb–Sb bond lengths are almost invariant of other structural parameters, which is indicative of strong covalent bonds; they vary in magnitude from 2.8427(13) to 2.8472(10) Å, and they are shorter than the 2.908 Å Sb–Sb distance found in elemental Sb [25]. The same can be said for the Bi–Bi bonding too, where the Bi–Bi distances are in the range 3.0443(8) to 3.0522(10) Å, which is shorter than the distances in elemental Bi [26]. However, this finding is not surprising, as similar values have been reported for KSb, Ba3Li4Bi4, Sr3Li4Sb4, Eu3Li4Sb4, KBi, SrLiBi, Ba21Cd4Bi18, and Eu4Li7Bi6 [13,20,27,28,29]. The Ba atoms prefer sites with high coordination numbers, and they can be viewed as Ba2+ cations residing within channels of the [Li7Sb6] and [Li7Bi6] polyanionic sub-structure (exaggerating of course the covalency of the Li–Sb and Li–Bi bonds).
We also draw attention to the Eu4Li6.60In0.40(1)Bi6 structure and that of Eu4Li7Bi6 as reported by our group in a previous study [13]. Rigorous assessment of the unit cell parameter and the interatomic distances show very clear differences, which attest to the structural response to the variation of the electron count (notice that the ionic radii of Li+ and In3+ for the same coordination number 4 are very close, 0.59 and 0.62 Å, respectively [30], and geometric factors will not be expected to play a big role, especially at this level or with Li–In substitution). First, let us compare the unit cell parameters and volumes. They are the following: a = 17.558(3) Å, b = 4.8114(8) Å, c = 12.812(2) Å, β =126.035(2)°, V = 875.2(3) Å3 for Eu4Li7Bi6, and a = 17.607(3) Å, b = 4.8222(8) Å, c = 12.826(2) Å, β =125.929(2)°, V = 881.8(2) Å3) for Eu4Li6.60In0.40(1)Bi6. The ca. 1% increase in the unit cell volume correlates well with some subtle changes in the bond distances and bond angles.
Overall, all bonds are slightly lengthened in the structure with the larger cell volume, Eu4Li6.60In0.40(1)Bi6, but identifying the most affected bonds is challenging, as many of the changes are within 3–5 e.s.d.s. For example, the Bi2 dumbbells elongate by 0.006(1) Å. Li–Bi interactions in the tetrahedral coordination are the ones that appear to show some statistically significant changes, which are mostly evident from the changes in bond angles. Focusing on the Li3 site, where the In substitution occurs, one can notice that while dLi3−Bi3 = 2.866(4) Å/dLi3−Bi2 = 2.990(3) Å in Eu4Li6.60In0.40(1)Bi6 are similar to dLi3−Bi3 = 2.86(3) Å/dLi3−Bi2 = 2.92(1) Å in Eu4Li7Bi6, the Bi2–Li3–Bi2 bond angles are slightly different, 107.5(1)° for the former structure and 111.0(8)° for the latter, meaning a slightly different type of tetrahedral distortion in either case.

2.2. Crystal Structure and Bonding in Ba7Li11Bi10

The new compound, Ba7Li11Bi10, was discovered and synthesized for the first time from stoichiometric reactions of the elements as part of this study. Ba7Li11Bi10 crystallizes with its own structure type, the Pearson index mS56 (Table 5). It is structurally related to the aforementioned “4-7-6” structures, which have 9 independent atomic positions (four for alkaline/rare-earth metals, three for the pnictogen atoms, and four for lithium atoms) in the asymmetric unit, while the Ba7Li11Bi10 structure has 15 symmetry-unique positions (four for barium atoms, five for the bismuth atoms, and six for lithium atoms) in the asymmetric unit. The Wyckoff sequence for this new crystallographic arrangement is i13 d a. Consequently, the structure is rather complex (Figure 2). A common trait is shared between the Ba4(Li1−xInx)7Bi6 and Ba7Li11Bi10 structures. They both have anionic substructures based on isolated Bi3− ions and [Bi2]4− dimers. The positions of the Li atoms in the two structures are such that the LiBi4 tetrahedra have similar connectivity, and the interatomic distances are closely matching (Table 4 and Table 6).
The observed average Li–Bi distances range between 2.799(9) Å to 3.071(2) Å, and 2.96(3) Å to 3.10(2) Å, for the Ba4(Li1−xInx)7Bi6 and Ba7Li11Bi10 structures, respectively. These values are in close range with the sum of the Pauling covalent radii; rLi + rBi = 1.225 Å + 1.510 Å [24], as well as with those reported for other compounds [13,20,27,28,29]. The tetrahedra are slightly distorted in both structures with the values for the Bi1–Li1–Bi2/Bi1–Li2–Bi3 bond angles ranging between 104.7(4)° and 111.8(3)°.
Similar arguments used above can be applied to the LiBi6 octahedra, where the average Li–Bi bond distances in the Ba4(Li1−xInx)7Bi6 and Ba7Li11Bi10 structures range between 3.4419(5) Å and 3.4407(4) Å for the former, and between 3.4274(6) Å and 3.4398(8) Å for the latter. In general, the bond lengths in the octahedra are longer than those in tetrahedral, as expected. The lengths of the Bi–Bi bonds in the Ba4(Li1−xInx)7Bi6 and Ba7Li11Bi10 structures match within two e.s.d.s.

2.3. Structural Relationships

Considering the similarities between the “4-7-6” and “7-11-10” structures, it can be proposed that the two are members of a homologous series. Let us illustrate this idea by taking two compounds with known structures—Ba3Li4Bi4 (Zr3Cu4Si4 structure type, Pearson symbol oI44) and BaLi3Bi2 (LaLi3Sb2 structure type, filled version of the CaAl2Si2 structure type, Pearson symbol hP6). We draw attention to the fact that the existence of the former compound has been experimentally confirmed, but the latter is not known. For electronic stability reasons, as discussed in the next section, BaLi3Bi2 is not likely to form, and its closest analog would be EuLi2.58In0.42(2)Bi2, which was obtained as a part of this study (see the Supplementary Materials). For comparison, the isotypic lanthanide-based RELi3Bi2 are valance-precise semiconductors, whose formulae can be represented as (RE3+)(Li1+)3(Bi3−)2, and they can be readily made [31]). Nonetheless, for the purposes of this discussion, BaLi3Bi2, even as a hypothetical case, will be considered, and slabs cut out from Ba3Li4Bi4 and BaLi3Bi2 can be integrated to form Ba4Li7Bi6 following Equation (1):
Ba3Li4Bi4 + BaLi3Bi2 = Ba4Li7Bi6
A detailed description of the structural relationships that equation 1 describes is already discussed in the literature [13]. Now, using the same two fragments, the structure of Ba7Li11Bi10 can be seen as realized through Equation (2):
2 × Ba3Li4Bi4 + BaLi3Bi2 = Ba7Li11Bi10
In other words, Ba4Li7Bi6 and Ba7Li11Bi10 are the simplest members of the family described with the general formula (BaLi3Bi2)n(Ba3Li4Bi4)m, where the Ba4Li7Bi6 is the member with n = 1 and m = 1, and Ba7Li11Bi10 is the intergrowth of the two components with n = 1 and m = 2, respectively. A pictorial representation of this analogy is shown in Figure 3.
The illustrated idea allows for the prediction of other possible members. For example, switching the ratio, i.e., taking the two components with n = 2 and m = 1, leads to Ba5Li10Bi8 = (BaLi3Bi2)2(Ba3Li4Bi4)1. Going above and beyond, based on this, one can envision the existence of other higher-order analogs such as Ba6Li13Bi10 (n = 3 and m = 1) or Ba10Li15Bi14 (n = 1 and m = 3). Experiments aimed at making these compounds were attempted, but so far they have been unsuccessful.
Another interesting structural relationship that can be mentioned here concerns the similarities between the structure of Ba4Li7Bi6 and that of Ba4Cd4Bi6 (=Ba2Cd2Bi3), which is actually not reported yet, but presumed to be isotypic with Ba2Cd2Sb3 (own type with the monoclinic space group C2/m and Pearson symbol mS28) [32]. The latter structure is described as a derivative of BaCd2Sb2 with the CaAl2Si2 structure type. Recall that the BaLi3Bi2 compound that we considered in our homologous series is the same basic structure, where an extra Li atom is inserted within. Given that Cd is nominally divalent, one can reason that the very same structure that is adopted by the Cd-bearing compound cannot be realized if Li (nominally monovalent) is used. Instead, the Ba2Li2Bi3 sub-structure can be seen as being distorted a little around the pivotal Bi2-dimers, which creates two more tetrahedral holes that are suitable for Li (described by one crystallographic position, Li2 in the notation used for the “4-7-6” structures—Figure 1). Still two electrons short of the ideal number of valence electrons, the imaginary Ba4Li6Bi6 accepts one more Li atom, in an octahedral hole (described by position Li4 in the notation used for the “4-7-6” structures). A pictorial representation of this analogy is shown in Figure 4.

2.4. Valence Electron Count and Electronic Band Structure

As mentioned earlier in this paper, Eu4Li7Bi6 does not appear to satisfy the Zintl–Klemm electron counting scheme [33], as attempts to rationalize the structure ((Eu2+)4(Li+)7([Bi2]4−)(Bi3−)4(h+), where h+ denotes an electron hole) fail to produce a charge-balanced formula [13]. In other words, the compound Eu4Li7Bi6, joins the ranks of electron-deficient “near” Zintl phases, such as the families of Ca14MnBi11 [34] and Ca9Zn4Sb9 [35]. The structure of the former has been experimentally confirmed to contain an electron hole, and it can be judiciously tuned to a Zintl phase by the aliovalent substitution of one Ca2+ cation by one RE3+ cation (RE = rare-earth metal), as demonstrated with the examples of Ca13REMnBi11 [36] and Ca13REMnSb11 [37]. On the other hand, the originally published Ca9Zn4Sb9 structure has been revisited, and an interstitial position within it has been identified, i.e., the formula is Ca9Zn4+xSb9 [38], which also brings the valence electron count very close to the expected from the Zintl concept. This structure has also been shown to be amenable to tuning via substitution, as demonstrated with the example of Ca8REMn4Sb9 [39], where the interstitial site is empty, but the electron count is modulated by the extra electron contributed by the rare-earth metal substituting for Ca.
On the opposite side of the spectrum, here are some nominally Zintl phases with the “wrong” electron count. Good examples are the structures of Ca4Bi2O (previously thought to be Ca2Bi) [40], and the unusual Ba5Cd2Sb5O0.5 [41]. For both of them, the perceived electron surplus has helped to identify the unrecognized oxygen impurity. Considering the ambivalent role that Li can play in intermetallics, we might bring up the case studies carried out on germanides/stannide with complex structures, such as AELi1−xInxGe2, RE4Li4−xSn4+x and Li9−xEuSn6+x [14,15,16], which show the tendency of such structures to attain more optimal valence electron counts by Li-group 13 or Li-group 14 element substitutions.
Armed with the knowledge from the above-mentioned studies, we considered many different hypotheses, to ultimately settle on the notion that the electron count for the “4-7-6” compounds needs to be augmented, which is achieved by virtue of substituting a fraction of the Li atoms with either Ga or In atoms. As seen from the total and partial density of states (DOS) curves of Ba4Li7Bi6 (Figure 5), the integrated DOS at the Fermi level (EF = 0 eV) corresponds to 45 valence electrons per unit cell. Note that the calculation is done on Ba4Li7Bi6, which is an ordered model of the actual Ba4(Li1−xInx)7Bi6 structure, where the mixed occupied Li/In site, according to the single-crystal structure refinement data, were treated as only occupied by Li atoms. A closer inspection shows that an additional electron is required to reach the top of the valence band, in analogy to the findings previously discussed for Eu4Li7Bi6 [13]. Thus, the electronic calculations are in excellent agreement with the formulation based on the Zintl–Klemm concept. Given the inability to prepare other pure ternary compounds with this structure with Ba or Sr, both of which can contribute only two electrons to the bonding, it can be surmised that the hypothetical Ba4Li7Bi6 cannot be realized, and that Ga or In doping on the Li site is critical to obtain more electronically stable, charge-balanced compounds.
Ba7Li11Bi10 is not an electron-precise compound either. According to Zintl concept, the empirical formula of Ba7Li11Bi10 can be broken down to (Ba2+)7(Li+)11([Bi2]4−)2(Bi3−)6(h+), which indicates a shortage of one electron per formula unit. This is not surprising, given that the building blocks of Ba4Li7Bi6 and Ba7Li11Bi10 are the same (vide supra). The total and partial density of states (DOS) curves of Ba7Li11Bi10 are shown in Figure 6, and agree with this conjecture—indeed, similar electronic characteristics can be noticed. For instance, both structures have non-zero DOS at the Fermi level, indicating metallic behavior. The s orbitals of Bi contribute almost exclusively to the energy DOS peaks in the −11 to −9.5 eV range, with the majority of them being lone pairs. Considering the very sharp bonding and antibonding peaks in the same energy range, as shown in the crystal orbital Hamilton population (COHP) in Figure 6b, the s orbitals of Bi are also responsible for the σ-bonding (and σ*-antibonding) states of the Bi2-dimer. The p orbitals of Bi are mixed with Ba and Li orbitals in the range between −3 eV to the Fermi level, suggesting the emergence of multiple covalent type interactions between these atoms.
The integrated DOS for Ba7Li11Bi10 (Figure 6) at EF = 0 eV corresponds to 75 valence electrons per unit cell. If the rigid band model is employed, integrating the DOS to 76 valence electrons, which is what the Zintl concept predicts, moves the Fermi level up in energy to a local DOS minimum at ca. 0.3 eV. This is perhaps the most notable difference between the electronic structures of Ba4Li7Bi6 and Ba7Li11Bi10, where an augmented electron count for the former leads to an electronic structure that is fully optimized, and a sizeable band-gap is opened, whereas for the latter, adding one more electron only helps to reach a nearly vanishing energy gap. This small difference might explain why doping in the Ba7Li11Bi10 structure is not as critical as it is for the Ba4Li7Bi6 counterpart, in line with the realization that, as discussed earlier, the Ba4Li7Bi6 structure might be seen as being made up of 50% BaLi3Bi2-fragments, which are electron-deficient by nature. By comparison, in Ba7Li11Bi10, the contribution of the electron-deficient BaLi3Bi2-component is reduced to one-third.
For a better understanding of the atomic interactions, the crystal orbital Hamilton population (COHP) curves were constructed and closely examined. In general, the bonding picture in herein is similar to what was previously described for the Eu4Li7Bi6 compound [13]. The bonding description here is valid for both Ba4Li7Bi6 and Ba7Li11Bi10 compounds. The COHP curve of the Bi–Bi dimers show antibonding character close to the Fermi level in addition to some deeper bonding states. For both structures, the values for the integrated –COHP for Bi–Bi interactions are essentially the same at the Fermi level (~1.6 eV per bond). Although a direct comparison between the bonding strengths of different linear muffin-tin orbital (LMTO) calculations is not valid, we can see that the magnitude of the Bi–Bi bonding interactions is approximately the same. Judging from the –COHPs, the antibonding π* and σ* states of the [Bi2] dimers derived from p-orbitals are not completely occupied, which may indicate that the bond order within the dimers is not 1, like in the I2 molecule to which an analogy was drawn earlier, but higher. The notion of a “double bond” is inconsistent with the lengths of the Bi–Bi bonds in both Ba4(Li1−xInx)7Bi6 and Ba7Li11Bi10 structures (Table 4 and Table 6, respectively), but partial/non-integer bond order is conceivable. Thus, the formulae Ba4Li7Bi6 and Ba7Li11Bi10 can be formally represented as (Ba2+)4(Li+)7([Bi2]3−(Bi3−)4 and (Ba2+)7(Li+)11([Bi2]3.5−)2(Bi3−)6, respectively. In this view, the idealized “4-7-6” compounds will have a higher bond order (i.e., 1.5) tan the “7-11-10” ones, but this difference is offset in the actual “4-7-6” compounds by the partial substitution of In or Ga for Li; hence, the formal charge of the [Bi2] moieties in both is about the same.
The Li–Bi bonds are optimized, reflecting the strong covalent nature, while the Ba–Bi interactions are slightly underoptimized (electron-deficient) because there are still bonding states available above the Fermi level. This situation will not change even by adding more electrons, i.e., moving the Fermi level up to the gap. This scenario is not unusual for highly polar interactions with strong ionic contribution [42]. Similarly, the Li–Bi will not change much if the Fermi level were shifted up because only a few states are available above the Fermi level and are of anti-bonding character for the Bi–Bi interactions and bonding for Li–Bi ones. We can estimate that for both structures, the integrated –COHP values for the Li–Bi interactions lie between 0.1 and 0.4 eV per bond, while for the Ba–Bi interactions, they range between 0.4 and 0.7 eV per bond.

3. Materials and Methods

3.1. Synthesis

Owing to their air-sensitivity, all of the starting materials and products were manipulated and stored in an Ar-filled glovebox (H2O, <1 ppm; O2, <1 ppm) or under a vacuum. All of the reagents had purities of greater than 99.9 wt %, and they were used as purchased from Sigma-Aldrich (Saint Louis, MO, USA) or Alfa Aesar (Tewksbury, NJ, USA). The surfaces of the lithium and barium rods were scraped clean before use. For direct solid-state reactions, mixtures of the starting elements in the desired stoichiometric ratios were weighed (~500 mg) and loaded into Nb tubes, arc-welded under an Ar atmosphere, and enclosed in evacuated fused silica ampoules to prevent oxidation upon heating to high temperatures. The reaction vessels were placed in high-temperature tube-furnaces with programmable controllers (Thermo Fisher Scientific, Waltham, MA, USA). Many batches of AE4(Li1−xGax)7Pn6 and AE4(Li1−xInx)7Pn6 (AE = Sr, Ba, Eu; Pn = Sb, Bi) samples were prepared with varied Li/Ga and Li/In ratios. From one such reaction aimed at Ba4(Li1−xGax)7Bi6, a compound with a new structure was identified, that of Ba7Li11Bi10. After the structure and composition were established, experiments were set up to make isotypic Ba7Li11Sb10, as well as AE7Li11Sb10 and AE7Li11Bi10 (AE = Sr, Eu), but they were not successful.
For all of the reported compounds, the reaction products were multi-phase mixtures, and therefore they could not be used for property measurements. Attempts to optimize the conditions for preparing the target compounds were made of course—in each system, several experiments with different temperature profiles were explored. The best synthesis route involved ramping the temperature to 860 °C at a rate of 300 °C/h, and then holding the temperature for 48 h, during which period, the ampoules were turned by hand several times to ensure sample homogeneity. The reaction mixtures were slowly cooled down to ambient temperature at a rate of −4 °C/h. The Nb tubes were brought into the glovebox and cut open. The typical products formed were polycrystalline, which under an inspection by optical microscope were seen to contain small irregularly-shaped crystals with silver luster. The polycrystalline materials are air-sensitive and samples left exposed to air were visually found to decompose within 24 h or less.
All reported structures were established by single-crystal X-ray crystallography. We need to mention here that almost all structurally characterized “4-7-6” samples are Ba-containing phases, and one contains Eu. There are no refined structures with Sr, although many specimens were prepared, but the crystals’ quality was inadequate for structure solution and refinement. For example, based on the obtained unit cell volume and partial structure solution, we are confident that Sr4(Li1−xGax)7Bi6 also exists (a = 17.750(7) Å, b = 4.846(2) Å, and c = 12.910(5) Å, β = 125.93(1)°). Note that since Sr2+ and Eu2+ have almost identical effective ionic sizes [30], the unit cell parameters of the structurally characterized Eu4(Li1−xInx)7Bi6 (a = 17.642(4) Å, b = 4.8297(10) Å, and c = 12.850(3) Å, β = 125.85(1)°) are a very close match to those of the speculated Sr4(Li1−xGax)7Bi6.
In the course of the study, several other new phases were serendipitously encountered. These include BaLiBi, Ba(Li1−xInx)2Bi2, Sr3Li3GaSb4, Sr3Li3InSb4, and Eu(Li1−xInx)Li2Bi2, among others that are still unknown. Structural work to fully elucidate the structures of the above-mentioned compounds is ongoing. Preliminary data for Eu(Li1−xInx)Li2Bi2 (isotypic to LaLi3Sb2, a “filled” variant of the CaAl2Si2-type) is given as Supplementary Materials, since this structure is a building block of the herein discussed “4-7-6” and “7-11-10” structures.

3.2. Powder X-Ray Diffraction

Room-temperature powder X-ray diffraction (PXRD) patterns of the raw reaction products were recorded in Bragg–Brentano geometry by the means of a Rigaku MiniFlex powder diffractometer (Rigaku Corporation, Tokyo, Japan) using nickel-filtered Cu Kα (λ = 1.5418 Å) radiation. Powder diffractograms were recorded in the 2θ range 5–75°, with a step size of 0.05° and 2 s/step counting time. The diffractometer was operated inside a nitrogen-filled glovebox to allow for data collection of air-sensitive samples. The collected powder X-ray diffraction patterns were only used to check the phase purity. This was performed using a JADE 6.5 software package (MDI, Livermore, CA, USA). Structure elucidation was done by means of single-crystal X-ray diffraction methods.

3.3. Single-Crystal X-Ray Diffraction

Single-crystal X-ray diffraction data were collected on a Bruker APEX-II CCD-based diffractometer with graphite-monochromated Mo Kα (λ = 0.71073 Å) radiation equipped with a low-temperature apparatus (Bruker AXS, Madison, WI, USA). The measurements were carried out at a steady temperature of 200 K. Prior to the data collection, a few crystals were selected from each sample batch, cut in Paratone N oil to the desired dimensions, mounted on glass fibers, and checked for quality. The program Bruker APEX2 was used for data collection, while cell refinement and data reduction were performed using the Bruker SAINT program [43]. Semi-empirical absorption correction based on equivalent reflections was applied with SADABS [44]. The structures were solved by the SHELXS structure solution program using direct methods, while the refinements were performed by SHELXL using least-squares minimization [45,46]. Atomic coordinates were standardized using the STRUCTURE TIDY program [47]. The final positional coordinates and displacement parameters from all refined structures are displayed in Table 7 and Table 8.
Multiple data collections and structure solution and refinements were carried out, in part, to ensure reproducibility, and in part, as a result of some problems with refining the displacement parameters and/or occupation factors of the very light Li atoms, especially when the heavy Ba and Bi are in near proximity. Specifically, the Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6 structures have four crystallographically distinct sites, one of which is a special position. The Ba7Li11Bi10 structure has two additional Li sites, six in total, and one of which is also on a special position with fixed coordinates. The refinement of the heavy elements in each case proceeded smoothly. However, refining the Li atoms, particularly when the refinements were attempted with anisotropic atomic displacement parameters proved difficult. Those problems are believed to originate from crystal quality issues and/or inadequate correction for absorption, as evidenced from the data gathered in Table 2, Table 3 and Table 5. Therefore, in some refined structures, some or all Li atoms are refined with isotropic atomic displacement parameters; in some instances, to ensure convergence, constraints may have been applied as well. The site occupancy factors (SOF) for all of the atoms in each compound were refined independently to verify the presence/lack of crystallographic ordering, and in the cases of the “doped” Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6, particular attention was paid to the SOFs of the Li positions. From the multiple refinements for crystals from different batches, it was established that the Li1, Li2, and Li4 positions in the structures of the above-mentioned compounds were fully occupied, while the Li3 positions revealed excess electron densities with SOFs often exceeding the scattering power of elemental Li by ca. 300–500%. The latter were treated as being mixed-occupied with In or Ga, and the refinement of structures from crystals selected from different batches revealed small compositional variations, concomitant with small changes in the unit cell constants, suggesting possible homogeneity ranges. Similar kinds of Li–In, Li–Ge, or Li–Sn disorder have been discussed in other publications [14,15,16,17,48].
The refinements of Ba7Li11Bi10 (and its targeted Ga-doped version, Table 5) showed that the heavy atoms were well behaved, whereas at least three of the six crystallographic distinct Li sites exhibited problems—their thermal parameters could not be refined anisotropically in some cases, and in addition, there were high uncertainties, even when they were refined isotropically. The Li6 site (special position) showed an occupation factor exceeding unity (sometimes by almost 50–60%) when freed, even in the sample that was prepared from an elemental mixture of Ba, Li, and Bi only, i.e., it was not deliberately doped with Ga. Such presumed excess electron density on the Li6 site is very difficult to explain, and most likely due to inadequate crystal quality, as multiple data collections showed great variations in the refinements of all Li sites, and of Li6 in particular. This, combined with the fact that the unit cell volume appears to be invariant of the synthesis route, and that the changes upon the introduction of a dopant element are negligible, is indirect proof that the Ba7Li11Bi10 structure is not as susceptible to alteration as the structures of Ba4(Li1−xGax)7Sb6, Ba4(Li1−xInx)7Sb6, Ba4(Li1−xInx)7Bi6, and Eu4(Li1−xInx)7Bi6.
CSD 1867165, 1867166, 1867167, 1867168 and 1867169 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html (or from the CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44 1223 336033; E-mail: [email protected]).

3.4. Electronic Structure Calculations

The electronic structure calculations for Ba4Li7Bi6 and Ba7Li11Bi10 compounds were performed using the tight-binding linear muffin-tin orbital (TB-LMTO) method with atomic spheres approximation (ASA), using the TB-LMTO-ASA 4.7 program [49]. The von Barth-Hedin LDA functional [50] was employed and the Brillouin zone was sampled by 78 and 310 k-points sets for the Ba4Li7Bi6 and Ba7Li11Bi10 structures, respectively. The density of states (DOS) and the crystal orbital Hamilton population (COHP) were evaluated using the automatic procedure in the LMTO code.

4. Conclusions

In the course of this study we discovered many new members of the series of compounds based on the “4-7-6” structure [13], as well as the novel compound Ba7Li11Bi10. The “4-7-6” and “7-11-10” structures are homologues, and can be formally considered as being built from the same building block. This modular approach can be further extended for other pnictides.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/6/4/109/s1, Figure S1: Polyhedral representation of the crystal structure of EuLi2.58In0.42(2)Bi2, Table S1: Selected crystal structure data and refinement parameters for EuLi2.58In0.42(2)Bi2, Table S2: Final refined positional coordinates and displacement parameters for EuLi2.58In0.42(2)Bi2, A combined CIF and checkCIF for all discussed structures.

Author Contributions

D.O.O., investigation; S.B., resources; D.O.O., writing—original draft preparation; S.B., writing—review and editing; S.B., supervision; S.B., project administration.

Funding

This research was funded by U.S. Department of Energy, Office of Science, Basic Energy Sciences, Award # DE-SC0008885.

Acknowledgments

We express gratitude to Yi Wang for the synthesis of some Ba4(Li1−xInx)7Sb6 samples and Alexander Ovchinnikov for assistance with the electronic band structure calculations. The authors are also indebted to the anonymous reviewer who made very helpful suggestions regarding the interpretation of the computational results.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
  2. Xu, Z.; Guloy, A.M. Ca5In9Sn6: Interplay of structural and electronic factors between intermetallic and Zintl phases. J. Am. Chem. Soc. 1998, 120, 7349–7350. [Google Scholar] [CrossRef]
  3. Chan, J.Y.; Kauzlarich, S.M.; Klavins, P.; Liu, J.; Shelton, R.N.; Webb, D.J. Synthesis, magnetic properties, and colossal magnetoresistance of Eu13.97Gd0.03MnSb11. Phys. Rev. B 2000, 61, 459–463. [Google Scholar] [CrossRef]
  4. Zevalkink, A.; Swallow, J.; Snyder, G.J. Thermoelectric properties of Zn-doped Ca5In2Sb6. Dalton Trans. 2013, 42, 9713–9719. [Google Scholar] [CrossRef] [PubMed]
  5. Park, S.-M.; Choi, E.S.; Kang, W.; Kim, S.-J. Eu5In2Sb6, Eu5In2−xZnxSb6: rare earth Zintl phases with narrow band gaps. J. Mater. Chem. 2002, 12, 1839–1843. [Google Scholar] [CrossRef]
  6. Brown, S.R.; Kauzlarich, S.M.; Gascoin, F.; Snyder, J.G. Yb14MnSb11: New high efficiency thermoelectric material for power generation. Chem. Mater. 2006, 18, 1873–1877. [Google Scholar] [CrossRef]
  7. Yan, Y.L.; Wang, Y.X.; Zhang, G.B. Electronic structure and thermoelectric performance of Zintl compound Ca5Ga2As6. J. Mater. Chem. 2012, 22, 20284–20290. [Google Scholar] [CrossRef]
  8. Zevalkink, A.; Toberer, E.S.; Bleith, T.; Flage-Larsen, E.; Snyder, G.J. Improved carrier concentration control in Zn-doped Ca5Al2Sb6. J. Appl. Phys. 2011, 110, 013721. [Google Scholar] [CrossRef]
  9. Makongo, J.P.A.; You, T.S.; He, H.; Suen, N.-T.; Bobev, S. New lithium-containing pnictides with 1-D infinite chains of supertetrahedral clusters: Synthesis, crystal and electronic structure of Ba4Li2Cd3Pn6 (Pn = P, As and Sb). Eur. J. Inorg. Chem. 2014, 2014, 5113–5124. [Google Scholar] [CrossRef]
  10. Wang, Y.; Stoyko, S.; Bobev, S. Quaternary pnictides with complex, noncentrosymmetric structures. Synthesis and structural characterization of the new Zintl phases Na11Ca2Al3Sb8, Na4CaGaSb3, and Na15Ca3In5Sb12. Inorg. Chem. 2015, 54, 1931–1939. [Google Scholar] [CrossRef] [PubMed]
  11. Xia, S.-Q.; Hullmann, J.; Bobev, S. Gallium substitutions as a means to stabilize alkaline-earth and rare-earth metal pnictides with the cubic Th3P4 type: Synthesis and structure of A7Ga2Sb6 (A = Sr, Ba, Eu). J. Solid State Chem. 2008, 181, 1909–1914. [Google Scholar] [CrossRef]
  12. He, H.; Tyson, C.; Saito, M.; Bobev, S. Synthesis and structural characterization of the ternary Zintl phases AE3Al2Pn4 and AE3Ga2Pn4 (AE = Ca, Sr, Ba, Eu; Pn = P, As). J. Solid State Chem. 2012, 188, 59–65. [Google Scholar] [CrossRef]
  13. Schäfer, M.C.; Suen, N.-T.; Bobev, S. Synthesis and crystal chemistry of new ternary pnictides containing lithium—Adding structural complexity one step at a time. Dalton Trans. 2014, 43, 16889–16901. [Google Scholar] [CrossRef] [PubMed]
  14. You, T.-S.; Bobev, S. Cis-trans Germanium chains in the intermetallic compounds ALi1−xInxGe2 and A2(Li1−xInx)2Ge3 (A = Sr, Ba, Eu)—Experimental and theoretical studies. J. Solid State Chem. 2010, 183, 2895–2902. [Google Scholar] [CrossRef]
  15. Suen, N.-T.; Guo, S.-P.; Hoos, J.; Bobev, S. Intricate Li–Sn disorder in rare-earth metal–lithium stannides. Crystal chemistry of RE3Li4−xSn4+x (RE = La–Nd, Sm; x <0.3) and Eu7Li8−xSn10+x. Inorg. Chem. 2018, 57, 5632–5641. [Google Scholar] [PubMed]
  16. Todorov, I.; Sevov, S.C. Heavy-metal aromatic and conjugated species: Rings, oligomers, and chains of tin in Li9−xEuSn6+x, Li9−xCaSn6+x, Li5Ca7Sn11, Li6Eu5Sn9, LiMgEu2Sn3, and LiMgSr2Sn3. Inorg. Chem. 2005, 44, 5361–5369. [Google Scholar] [CrossRef] [PubMed]
  17. Todorov, I.; Sevov, S.C. Synthesis and characterization of Na2Ba4Ga2Sb6 and Li13Ba8GaSb12. Z. Kristallogr. 2006, 221, 319–333. [Google Scholar] [CrossRef]
  18. Suen, N.-T.; Bobev, S. Several new phases in RE–Mg–Ge systems (RE = rare-earth metal)—Syntheses, structures, and chemical bonding. Eur. J. Inorg. Chem. 2012, 4141–4148. [Google Scholar] [CrossRef]
  19. Monconduit, L.; Belin, C. A new ternary antimonide phase, LiBaSb. Acta Crystallogr. 2001, E57, i17–i18. [Google Scholar] [CrossRef]
  20. Gupta, S.; Ganguli, A.K. Synthesis, structure and properties of a new Zintl phase: SrLiSb. J. Solid State Chem. 2006, 179, 1318–1322. [Google Scholar] [CrossRef]
  21. Liebrich, O.; Schäfer, H.; Weiss, A. Darstellung und Kristallstruktur von Sr3Li4Sb4 und Ba3Li4Sb4. Z. Naturforsch. B 1966, 25b, 650–651. [Google Scholar] [CrossRef]
  22. Eisenmann, B.; Liebrich, O.; Schäfer, H.; Weiss, A. Darstellung und Kristallstruktur von CaLiSb. Z. Naturforsch. B 1969, 24, 1344–1345. [Google Scholar] [CrossRef]
  23. Eisenmann, B.; Schäfer, H.; Turban, K. Neue intermetallische Verbindungen im anti-PbCl2Typ. Z. Naturforsch. B 1975, 30, 677–680. [Google Scholar] [CrossRef]
  24. Pauling, L. The Nature of the Chemical Bond; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
  25. Barrett, C.S.; Cucka, P.; Haefner, K. The crystal structure of antimony at 4.2, 78 and 298 K. Acta Crystallogr. 1963, 16, 451–453. [Google Scholar] [CrossRef]
  26. Cucka, P.; Barrett, C.S. The crystal structure of Bi and of solid solutions of Pb, Sn, Sb and Te in Bi. Acta Crystallogr. 1962, 15, 865–872. [Google Scholar] [CrossRef]
  27. Hönle, W.; von Schnering, H. Zur Struktur von LiP und KSb. Z. Kristallogr. 1981, 155, 307–314. [Google Scholar] [CrossRef]
  28. Xia, S.-Q.; Bobev, S. Zintl phase variations through cation selection. Synthesis and structure of A21Cd4Pn18 (A = Eu, Sr, Ba; Pn = Sb, Bi). Inorg. Chem. 2008, 47, 1919–1921. [Google Scholar] [CrossRef] [PubMed]
  29. Emmerling, F.; Längin, N.; Petri, D.; Kroeker, M.; Röhr, C. Alkalimetallbismutide ABi und ABi2 (A = K, Rb, Cs)—Synthesen, Kristallstrukturen, Eigenschaften. Z. Anorg. Allg. Chem. 2004, 630, 171–178. [Google Scholar] [CrossRef]
  30. Shannon, R.D. Effective ionic radii in oxides and fluorides. Acta Crystallogr. 1969, B25, 925–946. [Google Scholar] [CrossRef]
  31. Prakash, J.; Schäfer, M.C.; Bobev, S. Synthesis and structure determination of seven ternary bismuthides. Crystal chemistry of the RELi3Bi2 family (RE = La–Nd, Sm, Gd, Tb). Acta Crystallogr. 2015, C71, 894–899. [Google Scholar]
  32. Saparov, B.; He, H.; Zhang, X.; Greene, R.; Bobev, S. Synthesis, crystallographic and theoretical studies of the new Zintl phases Ba2Cd2Pn3 (Pn = As, Sb), and the solid solutions (Ba1−xSrx)2Cd2Sb3 and Ba2Cd2(Sb1−xAsx)3. Dalton Trans. 2010, 39, 1063–1070. [Google Scholar] [CrossRef] [PubMed]
  33. Guloy, A.M. Inorganic Chemistry in Focus III; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
  34. Rehr, A.; Kuromoto, T.Y.; Kauzlarich, S.M.; Del Castillo, J.; Webb, D.J. Structure and properties of the transition-metal Zintl compounds A14MnPn11 (A = Ca, Sr, Ba; Pn = As, Sb). Chem. Mater. 1994, 6, 93–99. [Google Scholar] [CrossRef]
  35. Brechtel, E.; Cordier, G.; Schäfer, H. Darstellung und Kristallstruktur von Ca9Mn4Bi9 und Ca9Zn4Bi9. Z. Naturforsch. B 1979, 34, 1229–1233. [Google Scholar] [CrossRef]
  36. Ovchinnikov, A.; Prakash, J.; Bobev, S. Crystal chemistry and magnetic properties of the solid solutions Ca14−xRExMnBi11 (RE = La–Nd, Sm, and Gd–Ho; x ≈ 0.6–0.8). Dalton Trans. 2017, 46, 16041–16049. [Google Scholar] [CrossRef] [PubMed]
  37. Prakash, J.; Stoyko, S.; Voss, L.; Bobev, S. On the extended series of quaternary Zintl phases Ca13REMnSb11 (RE = La–Nd, Sm, Gd–Dy). Eur. J. Inorg. Chem. 2016, 2912–2922. [Google Scholar] [CrossRef]
  38. Xia, S.-Q.; Bobev, S. Interplay between size and electronic effects in determining the homogeneity range of the A9Zn4+xPn9 and A9Cd4+xPn9 Phases (0 ≤ x ≤ 0.5), A = Ca, Sr, Yb, Eu; Pn = Sb, Bi. J. Am. Chem. Soc. 2007, 129, 10011–10018. [Google Scholar] [CrossRef] [PubMed]
  39. Wang, Y.; Bobev, S. Rare-earth Metal Substitutions in Ca9−xRExMn4Sb9 (RE = La–Nd, Sm; x ≈ 1). Synthesis and characterization of a new series of narrow-gap semiconductors. Chem. Mater. 2018, 30, 3518–3527. [Google Scholar] [CrossRef]
  40. Xia, S.-Q.; Bobev, S. On the existence of Ca2Bi—Crystal and electronic structure of Ca4Bi2O. J. Alloys Compd. 2007, 427, 67–72. [Google Scholar] [CrossRef]
  41. Saparov, B.; Bobev, S. Synthesis, crystal and electronic structures of the new quaternary phases A5Cd2Sb5F (A = Sr, Ba, Eu), and Ba5Cd2Sb5Ox (0.5 < x < 0.7). Dalton Trans. 2010, 39, 11335–11343. [Google Scholar] [PubMed]
  42. Ovchinnikov, A.; Saparov, B.; Xia, S.-Q.; Bobev, S. The ternary alkaline-earth metal manganese bismuthides Sr2MnBi2 and Ba2Mn1−xBi2 (x ≈ 0.15). Inorg. Chem. 2017, 56, 12369–12378. [Google Scholar] [CrossRef] [PubMed]
  43. Bruker. SAINT; Version 8.34a; Bruker Analytical X-ray Systems Inc.: Madison, WI, USA, 2013. [Google Scholar]
  44. Sheldrick, G.M. SADABS; Version 2.10; Bruker Analytical X-ray Systems Inc.: Madison, WI, USA, 2001. [Google Scholar]
  45. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. 2015, C71, 3–8. [Google Scholar]
  46. Sheldrick, G.M. SHELXT-Integrated space-group and crystal-structure determination. Acta Crystallogr. 2015, A71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  47. Gelato, L.M.; Parthé, E. STRUCTURE TIDY—A computer program to standardize crystal structure data. J. Appl. Crystallogr. 1987, 20, 139–143. [Google Scholar] [CrossRef]
  48. Li, B.; Corbett, J.D. Phase stabilization through electronic tuning: Electron-poorer alkali-metal-indium compounds with unprecedented In/Li clusters. J. Am. Chem. Soc. 2005, 127, 926–932. [Google Scholar] [CrossRef] [PubMed]
  49. Jepsen, O.; Burkhart, A.; Andersen, O.K. The TB-LMTO-ASA Program, Version 4.7; Max-Planck-Institut für Festkörperforschung: Stuttgart, Germany, 1999. [Google Scholar]
  50. Von Barth, U.; Hedin, L. A local exchange-correlation potential for the spin polarized case: I. J. Phys. C Solid State Phys. 1972, 5, 1629–1642. [Google Scholar] [CrossRef]
Inorganics 06 00109 g001 550
Figure 1. (a) Polyhedral representation of the crystal structure of the “4-7-6” family of pnictides, viewed down the crystallographic b-axis. The unit cell is outlined. The data used to represent the structure are taken from the refinement of Ba4Li6.55In0.45(1)Bi6. Different types of atoms are differentiated as follows: Ba atoms are shown in medium-green, the Bi atoms are in orange, the Li atoms in tetrahedral coordination are drawn in yellow (Li1 and Li3, remnants of the “1-3-2” slab) and light blue (Li2, remnants of the “3-4-4” slab), while the Li atoms in octahedral coordination are depicted in light-green. (b) Ball-and-stick representation of the same structure in the same projection.
Figure 1. (a) Polyhedral representation of the crystal structure of the “4-7-6” family of pnictides, viewed down the crystallographic b-axis. The unit cell is outlined. The data used to represent the structure are taken from the refinement of Ba4Li6.55In0.45(1)Bi6. Different types of atoms are differentiated as follows: Ba atoms are shown in medium-green, the Bi atoms are in orange, the Li atoms in tetrahedral coordination are drawn in yellow (Li1 and Li3, remnants of the “1-3-2” slab) and light blue (Li2, remnants of the “3-4-4” slab), while the Li atoms in octahedral coordination are depicted in light-green. (b) Ball-and-stick representation of the same structure in the same projection.
Inorganics 06 00109 g001
Inorganics 06 00109 g002 550
Figure 2. (a) Polyhedral representation of the crystal structure of Ba7Li11Bi10, viewed down the crystallographic b-axis. Color codes of the atoms are the same as in Figure 1. (b) Ball-and-stick representation of the same structure in the same projection. The unit cell is outlined.
Figure 2. (a) Polyhedral representation of the crystal structure of Ba7Li11Bi10, viewed down the crystallographic b-axis. Color codes of the atoms are the same as in Figure 1. (b) Ball-and-stick representation of the same structure in the same projection. The unit cell is outlined.
Inorganics 06 00109 g002
Inorganics 06 00109 g003 550
Figure 3. Schematic illustration of the structural relationship between Ba7Li11Bi10 and Ba4Li7Bi6, which are considered as intergrowths of the same type of fragments. The slabs cut out from Ba3Li4Bi4 (Zr3Cu4Si4 structure type) are highlighted in light-blue, and the slabs derived from BaLi3Bi2 (LaLi3Sb2 structure type) are highlighted in yellow.
Figure 3. Schematic illustration of the structural relationship between Ba7Li11Bi10 and Ba4Li7Bi6, which are considered as intergrowths of the same type of fragments. The slabs cut out from Ba3Li4Bi4 (Zr3Cu4Si4 structure type) are highlighted in light-blue, and the slabs derived from BaLi3Bi2 (LaLi3Sb2 structure type) are highlighted in yellow.
Inorganics 06 00109 g003
Inorganics 06 00109 g004 550
Figure 4. Schematic illustration of the structural relationship between the Ba2Cd2Sb3 (a) and Eu4Li7Bi6 (b) structure types, which both crystallize in the same monoclinic space group C2/m. The three “empty” holes in imaginary Ba4Li4Bi6 (=Ba2Li2Bi3) that can be filled with Li atoms to yield Ba4Li7Bi6 are emphasized. Octahedral positions are in green, tetrahedral ones are in light-blue, in accordance with the color coding for the other figures.
Figure 4. Schematic illustration of the structural relationship between the Ba2Cd2Sb3 (a) and Eu4Li7Bi6 (b) structure types, which both crystallize in the same monoclinic space group C2/m. The three “empty” holes in imaginary Ba4Li4Bi6 (=Ba2Li2Bi3) that can be filled with Li atoms to yield Ba4Li7Bi6 are emphasized. Octahedral positions are in green, tetrahedral ones are in light-blue, in accordance with the color coding for the other figures.
Inorganics 06 00109 g004
Inorganics 06 00109 g005 550
Figure 5. (a) Projected total and partial density of states (DOS) for Ba4Li7Bi6. The partial DOS curves illustrate the contribution of different atoms to the total DOS (EF = 0 eV). (b) Crystal orbital Hamilton population (COHP) plots for Ba–Bi, Li–Bi and Bi–Bi interactions shown on the same energy scale. The COHP values are inverted, which is done so that “−” and “+” denote the antibonding and bonding regions, respectively.
Figure 5. (a) Projected total and partial density of states (DOS) for Ba4Li7Bi6. The partial DOS curves illustrate the contribution of different atoms to the total DOS (EF = 0 eV). (b) Crystal orbital Hamilton population (COHP) plots for Ba–Bi, Li–Bi and Bi–Bi interactions shown on the same energy scale. The COHP values are inverted, which is done so that “−” and “+” denote the antibonding and bonding regions, respectively.
Inorganics 06 00109 g005
Inorganics 06 00109 g006 550
Figure 6. (a) Projected total and partial DOS for Ba7Li11Bi10. The partial DOS curves illustrate the contribution of different atoms to the total DOS (EF = 0 eV). (b) The reversed COHP plots for Ba–Bi, Li–Bi and Bi–Bi interactions shown on the same energy scale.
Figure 6. (a) Projected total and partial DOS for Ba7Li11Bi10. The partial DOS curves illustrate the contribution of different atoms to the total DOS (EF = 0 eV). (b) The reversed COHP plots for Ba–Bi, Li–Bi and Bi–Bi interactions shown on the same energy scale.
Inorganics 06 00109 g006
Table
Table 1. Selected crystal structure data and refinement parameters for Ba4(Li1−xGax)7Sb6 a.
Table 1. Selected crystal structure data and refinement parameters for Ba4(Li1−xGax)7Sb6 a.
Empirical FormulaBa4Li6.65Ga0.35(1)Sb6
Formula weight, g·mol−11356.69
Space group, ZC2/m (No.12), 2
λ, Å0.71073
T, K200(2)
a, Å18.105(6)
b, Å4.9319(15)
c, Å13.023(4)
β, °126.676(4)
V, Å3932.6(5)
ρcalc, g·cm−34.83
µMo Kα, cm−1174.5
Collected/independent reflections5282/1162
Rint0.0361
GOF on F21.042
R1 (I > 2σ(I)) b0.0249
R1 (all data) b0.0285
wR2 (I > 2σ(I)) b0.0526
wR2 (all data) b0.0536
Largest peak/hole, e−Å−31.36/−1.37
a This is the same compound, previously reported as Ba8Li13GaSb12, the structure of which was refined in non-standard coordinate settings [17], and as a result assigned erroneously in ICSD. Reported unit cell parameters for Ba8Li13GaSb12: a = 18.065(1) Å, b = 4.9407(10) Å, c = 13.012(1) Å, β = 126.73(1)°, V = 930.8(2) Å3. b R1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = [∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]]1/2, where w = 1/[σ2Fo2 + (0.0267P)2], and P = (Fo2 + 2Fc2)/3. A CIF has been deposited with reference number CSD 1867165.
Table
Table 2. Selected crystal structure data and refinement parameters for Ba4(Li1−xInx)7Sb6 and Ba4(Li1−xInx)7Bi6.
Table 2. Selected crystal structure data and refinement parameters for Ba4(Li1−xInx)7Sb6 and Ba4(Li1−xInx)7Bi6.
Empirical FormulaBa4Li6.25In0.75(1)Sb6Ba4Li6.45In0.55(1)Sb6Ba4Li6.45In0.55(1)Sb6Ba4Li6.55In0.45(1)Bi6Ba4Li6.60In0.40(1)Bi6
Formula weight g·mol−11409.351387.771387.431900.371894.97
Space group, ZC2/m (No.12), 2
λ, Å0.71073
T, K200(2)
a, Å18.172(5)18.149(3)18.146(3)18.409(1)18.440(3)
b, Å4.9546(14)4.9406(9)4.9397(9)5.0133(4)5.0092(7)
c, Å13.093(4)13.082(2)13.080(2)13.282(1)13.275(2)
β, °126.799(3)126.678(2)126.680(2)126.292(1)126.271(2)
V, Å3944.0(5)940.8(3)940.3(3)988.0(1)986.3(2)
ρcalc, g·cm−34.964.904.906.396.38
µMo Kα, cm−1174.9173.1173.2615.7615.8
Collected/independent reflections7140/14548997/16157141/11747507/12437524/1239
Rint0.02960.04670.03990.04910.0821
GOF on F21.0661.0601.0371.0391.064
R1 (I > 2σ(I)) a0.01870.02410.02200.02560.0368
R1 (all data) a0.02070.02890.02580.02780.0425
wR2 (I > 2σ(I)) a0.04100.05650.04910.06130.0904
wR2 (all data) a0.04200.05800.05040.06230.0936
Largest peak/hole, e−Å−32.17/−1.891.37/−1.361.20/−1.291.64/−1.482.75/−3.94
aR1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = [∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]]1/2, where w = 1/[σ2Fo2 + (AP)2 + (BP)], and P = (Fo2 + 2Fc2)/3; A, B are the respective weight coefficients (see CIF in the supporting information). CIF have also been deposited with reference numbers CSD 1867166 and 1867167 (one from each composition).
Table
Table 3. Selected crystal structure data and refinement parameters for Eu4(Li1−xInx)7Bi6.
Table 3. Selected crystal structure data and refinement parameters for Eu4(Li1−xInx)7Bi6.
Empirical FormulaEu4Li6.55In0.45(1)Bi6Eu4Li6.60In0.40(1)Bi6
Formula weight, g·mol−11958.851953.45
Space group, ZC2/m (No.12), 2
λ, Å0.71073
T, K200(2)
a, Å17.642(4)17.607(3)
b, Å4.8297(10)4.8222(8)
c, Å12.850(3)12.826(2)
β, °125.845(2)125.929(2)
V, Å3887.6(3)881.8(2)
ρcalc, g·cm−37.337.36
µMo Kα, cm−1736.7740.9
Collected/independent reflections8340/14916718/1113
Rint0.05060.0468
GOF on F21.0531.119
R1 (I > 2σ(I)) a0.02780.0251
R1 (all data) a0.03320.0287
wR2 (I > 2σ(I)) a0.05760.0598
wR2 (all data) a0.05920.0609
Largest peak/hole, e−Å−32.21/−2.351.52/−2.34
aR1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = [∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]]1/2, where w = 1/[σ2Fo2 + (AP)2 + (BP)], and P = (Fo2 + 2Fc2)/3; A, B are the respective weight coefficients (see CIF in the supporting information). A CIF has been deposited with reference number CSD 1867168.
Table
Table 4. Selected distances (Å) in crystal structures of the “4-7-6” family of pnictides a.
Table 4. Selected distances (Å) in crystal structures of the “4-7-6” family of pnictides a.
Atom PairBa4(Li1−xGax)7Sb6Ba4(Li1−xInx)7Sb6Ba4(Li1−xInx)7Bi6Eu4(Li1−xInx)7Bi6
AE1–Pn1(2×)3.5192(9)3.5243(6)3.5538(6)3.3772(6)
AE1–Pn2(1×)3.488(1)3.4998(8)3.5540(9)3.4113(8)
AE1–Pn3(2×)3.5058(9)3.5040(6)3.5444(6)3.3394(6)
AE1–Pn3(1×)3.552(1)3.5272(8)3.5801(9)3.3726(8)
AE2–Pn1(2×)3.572(1)3.5762(7)3.6487(6)3.5208(7)
AE2–Pn1(2×)3.563(1)3.5592(6)3.6301(6)3.4851(7)
AE2–Pn2(2×)3.5556(9)3.5682(6)3.6195(6)3.4671(6)
Pn1–Pn1(1×)2.843(1)2.847(1)3.0589(9)3.052(1)
Li1–Pn1(1×)3.036(1)3.09(1)3.06(2)2.95(2)
Li1–Pn2(1×)2.961(1)2.98(1)3.07(2)2.99(2)
Li1–Pn3(2×)2.851(7)2.844(6)2.896(9)2.799(9)
Li2–Pn1(1×)2.96(1)2.96(1)3.00(2)2.99(3)
Li2–Pn2(2×)2.915(7)2.913(7)2.977(9)2.84(1)
Li2–Pn2(1×)3.00(1)3.00(1)2.99(2)2.87(3)
Li3–Pn3(2×) b2.812(4)2.857(2)2.930(3)2.866(4)
Li3–Pn2(2×) b2.977(2)3.027(1)3.071(2)2.990(3)
Li4–Pn2(2×)3.317(1)3.3662(7)3.4419(5)3.3222(7)
Li4–Pn3(2×)3.3468(8)3.3842(5)3.4407(4)3.3827(5)
a The shown metrics are those from the refinements of Ba4Li6.55Ga0.45(1)Sb6, Ba4Li6.45In0.55(1)Sb6, Ba4Li6.45In0.55(1)Bi6, and Eu4Li6.60In0.40(1)Bi6, respectively. b Li3 is mixed-occupied with Ga or In.
Table
Table 5. Selected crystal structure data refinement parameters for Ba7Li11Bi10.
Table 5. Selected crystal structure data refinement parameters for Ba7Li11Bi10.
Empirical FormulaBa7Li11Bi10Ba7Li11Bi10Ba7Li10.95Ga0.05(2)Bi10
Formula weight, g·mol−13127.523127.523130.66
Space group, ZC2/m (No.12), 2
λ, Å0.71073
T, K200(2)
a, Å18.407(3)18.397(2)18.407(4)
b, Å5.0258(9)5.0247(6)5.0241(11)
c, Å18.353(3)18.345(2)18.349(4)
β, °104.426(3)104.417(2)104.395(3)
V, Å31644.3(5)1642.4(3)1643.6(6)
ρcalc, g·cm−36.326.326.33
µMo Kα, cm−1614.9615.7615.6
Collected/independent reflections9394/206310342/175312318/2061
Rint0.04140.04840.0608
GOF on F21.0541.0621.035
R1 (I > 2σ(I)) a0.02980.02990.0312
R1 (all data) a0.03990.04020.0400
wR2 (I > 2σ(I)) a0.06250.06060.0701
wR2 (all data) a0.06510.06590.0736
Largest peak/hole, e−Å−33.64/−2.695.85/−2.722.43/−2.58
aR1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = [∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]]1/2, where w = 1/[σ2Fo2 + (AP)2 + (BP)], and P = (Fo2 + 2Fc2)/3; A, B are the respective weight coefficients (see CIF in the supporting information). A CIF has been deposited with reference number CSD 1867169.
Table
Table 6. Selected distances (Å) in Ba7Li11Bi10.
Table 6. Selected distances (Å) in Ba7Li11Bi10.
Atom PairDistanceAtom PairDistance
Ba1–Bi1(1×)3.569(1)Li1–Bi1(1×)2.96(3)
Ba1–Bi3(2×)3.5611(8)Li1–Bi2(1×)3.08(3)
Ba1–Bi5(2×)3.5432(8)Li2–Bi1(1×)3.04(3)
Ba1–Bi5(1×)3.592(1)Li2–Bi3(1×)3.06(3)
Ba2–Bi2(2×)3.6552(8)Li3–Bi2(1×)3.03(3)
Ba2–Bi3(2×)3.6490(9)Li3–Bi4(2×)3.00(2)
Ba2–Bi4(2×)3.6202(8)Li4–Bi1(2×)3.08(1)
Ba3–Bi1(2×)3.6063(8)Li4–Bi5(1×)2.84(2)
Ba3–Bi2(2×)3.6726(9)Li4–Bi5(1×)2.90(2)
Ba3–Bi3(2×)3.6538(8)Li5–Bi1(2×)2.94(1)
Ba4–Bi2(4×)3.4850(5)Li5–Bi3(1×)3.10(2)
Ba4–Bi4(2×)3.5603(7)Li6–Bi1(1×)3.4398(8)
Bi2–Bi3(1×)3.0443(8)Li6–Bi5(2×)3.4274(6)
Table
Table 7. Final refined positional coordinates and displacement parameters for AE4(Li1−xGax)7Pn6 and AE4(Li1−xInx)7Pn6 (AE = Ba, Eu; Pn = Sb, Bi). The shown metrics are those from the refinements of Ba4Li6.55Ga0.45(1)Sb6, Ba4Li6.45In0.55(1)Sb6, Ba4Li6.45In0.55(1)Bi6, and Eu4Li6.60In0.40(1)Bi6, respectively.
Table 7. Final refined positional coordinates and displacement parameters for AE4(Li1−xGax)7Pn6 and AE4(Li1−xInx)7Pn6 (AE = Ba, Eu; Pn = Sb, Bi). The shown metrics are those from the refinements of Ba4Li6.55Ga0.45(1)Sb6, Ba4Li6.45In0.55(1)Sb6, Ba4Li6.45In0.55(1)Bi6, and Eu4Li6.60In0.40(1)Bi6, respectively.
AtomWyckoff SitexyzUisoa/Ueq, b Å2Occupancy
Ba4(Li1−xGax)7Sb6
Ba14i0.2613(1)00.6602(1)0.0108(2)1
Ba24i0.4295(1)00.0856(1)0.0119(1)1
Sb14i0.0856(1)00.1241(1)0.0100(2)1
Sb24i0.1580(1)00.8152(1)0.0134(2)1
Sb34i0.3973(1)00.5455(1)0.0124(2)1
Li14i0.0435(1)00.318(1)0.007(1) a1
Li24i0.2340(9)00.094(1)0.007(1) a1
Li3/Ga4i0.4136(3)00.3444(4)0.007(1) a0.833(4)/0.167
Li42c00½0.019(5)1
Ba4(Li1−xInx)7Sb6
Ba14i0.2615(1)00.6602(1)0.0118(1)1
Ba24i0.4295(1)00.0856(1)0.0119(1)1
Sb14i0.0854(1)00.1238(1)0.0105(1)1
Sb24i0.1599(1)00.8185(1)0.0126(1)1
Sb34i0.3949(1)00.5457(1)0.0118(1)1
Li14i0.0429(8)00.320(1)0.013(2) a1
Li24i0.2340(9)00.094(1)0.016(3) a1
Li3/In4i0.4144(1)00.3583(2)0.0144(6) a0.712(2)/0.288
Li42c00½0.045(6) a1
Ba4(Li1−xInx)7Bi6
Ba14i0.2596(1)00.6588(1)0.0196(2)1
Ba24i0.4301(1)00.0844(1)0.0192(2)1
Bi14i0.0898(1)00.1302(1)0.0184(1)1
Bi24i0.1590(1)00.8191(1)0.0199(2)1
Bi34i0.3942(1)00.5455(1)0.0199(2)1
Li14i0.046(1)00.319(2)0.007(2) a1
Li24i0.233(1)00.089(2)0.007(2) a1
Li3/In4i0.4135(2)00.3466(3)0.023(1) a0.770(4)/0.230
Li42c00½0.07(1) a1
Eu4(Li1−xInx)7Bi6
Eu14i0.2598(1)00.6626(1)0.0144(2)1
Eu24i0.4328(1)00.0855(1)0.0155(2)1
Bi14i0.0933(1)00.1334(1)0.0131(1)1
Bi24i0.1557(1)00.8181(1)0.0147(1)1
Bi34i0.3831(1)00.5375(1)0.0148(1)1
Li14i0.053(1)00.3259(5)0.004(4) a1
Li24i0.239(2)00.089(2)0.021(1) a1
Li3/In4i0.4205(3)00.3521(4)0.021(2) a0.802(5)/0.198
Li42c00½0.06(2) a1
a Isotropic refinement. b Ueq is defined as one third of the trace of the orthogonalized Uij tensor.
Table
Table 8. Final refined positional coordinates and displacement parameters for Ba7Li11Bi10.
Table 8. Final refined positional coordinates and displacement parameters for Ba7Li11Bi10.
AtomWyckoff SitexyzUisoa/Ueq, b Å2Occupancy
Ba14i0.2149(1)00.0934(1)0.0102(2)1
Ba24i0.2649(1)00.3502(1)0.0105(2)1
Ba34i0.4538(1)00.2467(1)0.0099(2)1
Ba42d0½½0.0093(2)1
Bi14i0.0705(1)00.1921(1)0.0100(1)1
Bi24i0.0866(1)00.6228(1)0.0091(1)1
Bi34i0.1945(1)00.7783(1)0.0097(1)1
Bi44i0.3455(1)00.5843(1)0.0099(1)1
Bi54i0.3833(1)00.0282(1)0.0103(1)1
Li14i0.073(1)00.354(1)0.015(5) a1
Li24i0.095(2)00.889(2)0.023(6) a1
Li34i0.180(1)00.508(2)0.018(6) a1
Li44i0.540(1)00.092(1)0.006(3) a1
Li54i0.646(1)00.249(1)0.006(3) a1
Li62a0000.006(3) a1
a Isotropic refinement. b Ueq is defined as one third of the trace of the orthogonalized Uij tensor.

Share and Cite

MDPI and ACS Style

Ojwang, D.O.; Bobev, S. Synthesis and Structural Characterization of Ba7Li11Bi10 and AE4(Li,Tr)7Pn6 (AE = Sr, Ba, Eu; Tr = Ga, In; Pn = Sb, Bi). Inorganics 2018, 6, 109. https://doi.org/10.3390/inorganics6040109

AMA Style

Ojwang DO, Bobev S. Synthesis and Structural Characterization of Ba7Li11Bi10 and AE4(Li,Tr)7Pn6 (AE = Sr, Ba, Eu; Tr = Ga, In; Pn = Sb, Bi). Inorganics. 2018; 6(4):109. https://doi.org/10.3390/inorganics6040109

Chicago/Turabian Style

Ojwang, Dickson O., and Svilen Bobev. 2018. "Synthesis and Structural Characterization of Ba7Li11Bi10 and AE4(Li,Tr)7Pn6 (AE = Sr, Ba, Eu; Tr = Ga, In; Pn = Sb, Bi)" Inorganics 6, no. 4: 109. https://doi.org/10.3390/inorganics6040109

APA Style

Ojwang, D. O., & Bobev, S. (2018). Synthesis and Structural Characterization of Ba7Li11Bi10 and AE4(Li,Tr)7Pn6 (AE = Sr, Ba, Eu; Tr = Ga, In; Pn = Sb, Bi). Inorganics, 6(4), 109. https://doi.org/10.3390/inorganics6040109

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop