Next Article in Journal
Molecular Theranostic Agents for Photodynamic Therapy (PDT) and Magnetic Resonance Imaging (MRI)
Next Article in Special Issue
Stabilization of Supramolecular Networks of Polyiodides with Protonated Small Tetra-azacyclophanes
Previous Article in Journal
Survey of the Geometric and Electronic Structures of the Key Hydrogenated Forms of FeMo-co, the Active Site of the Enzyme Nitrogenase: Principles of the Mechanistically Significant Coordination Chemistry
Previous Article in Special Issue
Solvent and Substituent Effects on the Phosphine + CO2 Reaction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 7
Issue 1
10.3390/inorganics7010009
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Hydrogen Bond versus Halogen Bond in HXOn (X = F, Cl, Br, and I) Complexes with Lewis Bases

by
David Quiñonero
* and
Antonio Frontera
Department of Chemistry, Universitat de les Illes Balears, Crta de Valldemossa km 7.5, 07122 Palma de Mallorca (Baleares), Spain
*
Author to whom correspondence should be addressed.
Inorganics 2019, 7(1), 9; https://doi.org/10.3390/inorganics7010009
Submission received: 31 December 2018 / Revised: 14 January 2019 / Accepted: 15 January 2019 / Published: 17 January 2019
(This article belongs to the Special Issue Novel Non-Covalent Interactions)
Browse Figures
Versions Notes

Abstract

:
We have theoretically studied the formation of hydrogen-bonded (HB) and halogen-bonded (XB) complexes of halogen oxoacids (HXOn) with Lewis bases (NH3 and Cl−) at the CCSD(T)/CBS//RIMP2/aug-cc-pVTZ level of theory. Minima structures have been found for all HB and XB systems. Proton transfer is generally observed in complexes with three or four oxygen atoms, namely, HXO4:NH3, HClO3:Cl−, HBrO3:Cl−, and HXO4:Cl−. All XB complexes fall into the category of halogen-shared complexes, except for HClO4:NH3 and HClO4:Cl−, which are traditional ones. The interaction energies generally increase with the number of O atoms. Comparison of the energetics of the complexes indicates that the only XB complexes that are more favored than those of HB are HIO:NH3, HIO:Cl−, HIO2:Cl−, and HIO3:Cl−. The atoms-in-molecules (AIM) theory is used to analyze the complexes and results in good correlations between electron density and its Laplacian values with intermolecular equilibrium distances. The natural bon orbital (NBO) is used to analyze the complexes in terms of charge-transfer energy contributions, which usually increase as the number of O atoms increases. The nature of the interactions has been analyzed using the symmetry-adapted perturbation theory (SAPT) method. The results indicate that the most important energy contribution comes from electrostatics, followed by induction.

Graphical Abstract

1. Introduction

The comprehension of noncovalent forces lays the foundations for the interdisciplinary field of catalysis, supramolecular, biological, and atmospheric chemistry [1]. The pathways of biological and chemical processes are frequently controlled by complex combinations of noncovalent interactions [2]. Thus, an accurate description of the interactions between molecules is mandatory to comprehensively advance the fields of biology, physics, and chemistry.
In addition, apart from hydrogen bonding [3,4,5,6,7], there are other kinds of noncovalent interactions that have been attracting much attention from the scientific community, especially in the last few years, namely tetrel [8,9,10], pnictogen [11], chalcogen [12,13], halogen [14,15], and aerogen [16] bonds. There is a common pattern in all these noncovalent contacts: an interaction between an electron-density-rich region of a molecule, acting as a Lewis base, with an electron-density-deficient region (tetrel, pnictogen, chalcogen, halogen, or aerogen atoms) of another molecule, acting as a Lewis acid, the latter corresponding to a region of lower electron density associated with a portion of the surface electrostatic potential of a system, known as σ-hole. The formation of a covalent bond or bonds causes an anisotropy of the charge distribution of the atom giving rise to these σ-holes [17,18]. Particularly, according to IUPAC [19], “A halogen bond occurs when there is evidence of a net attractive interaction between an electrophilic region associated with a halogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity.” Recently, halogen bonds have attracted considerable attention due to their having similar functions to hydrogen bonds. For instance, halogen bonds have been used in the recognition mechanism of chemical and biological molecules [20,21,22], drug design [23,24,25], organocatalysis [26,27,28], and material science [29,30,31].
Hypohalous acids are a very interesting class of compounds because they are often used as a model to analyze the competition between hydrogen and halogen bonding due to the presence of both the hydrogen bond donor and halogen bond donor in their structure. In this regard, complexes of hypohalous acids with nitrogenated bases [32], carbon monoxide [33], formaldehyde [34], thioformaldehyde [35] benzene [36], dimethylchalcogens [37], monobromamine [38], formamidine [39], phosphine derivatives [40,41], sulfur ylides [42], dimethylsulfoxide [43], and substituted carbonyl compounds [44] have been the subject of study. The hypohalous acids are powerful oxidizing agents involved in atmospheric chemistry that participate in many oxidation, hydroxylation, and epoxidation reactions [45] and in the depletion of the ozone layer [46,47]. They also play a role as oxidants in many pathophysiological processes and have antibacterial properties [48,49,50]. In addition, halogen oxoacids, such as HXO2 [51,52,53,54] and HXO3 [55,56,57] (X = Cl, Br, I), have been proposed as key intermediates in elementary reactions to decompose ozone.
Atmospheric reactive nitrogen compounds are of particular importance to the surface–atmosphere exchange over agricultural land. In this regard, NH3 is the primary contributor to atmospheric reactive nitrogen dry deposition [58]. The majority of NH3 emissions originate from livestock excreta and, to a lesser extent, from agricultural sources from the application of N-containing fertilizers [59,60]. As the primary basic gas in the atmosphere, NH3 also reacts with trace acidic gases, such as hydrogen chloride (HCl). The product of this reaction gives rise to the aerosol ammonium chloride (NH4Cl), which acts as scattering aerosol that alters the Earth’s total albedo and contributes significantly to regional and global climate [61].
Despite the extensive research on the comparison between hydrogen- and halogen-bonding interactions on hypohalous acid complexes, to the best of our knowledge, no theoretical and experimental studies involving interactions of hypohalous acids with a chloride ion and the rest of the halogen oxoacids with NH3 and Cl− are available in the literature. In this article, we aim to account for the formation of binary complexes between halogen oxoacids and either NH3 or Cl− by means of high-level ab initio calculations (CCSD(T)/CSB//RI-MP2/aug-cc-pVTZ). As two types of complexes can be formed (hydrogen-bonded or halogen-bonded), we analyze which one is more favored. The characterization of the interactions has been scrutinized by using the atoms-in-molecules (AIM) theory (electron density analysis, degree of covalency), the natural bon orbital (NBO) (charge transfer effects), and the symmetry-adapted perturbation theory (SAPT) method (energy partition).

2. Results and Discussion

2.1. Halogen Oxoacids

Initially, we compared our computed geometries of the halogen oxoacids with experimental evidence. However, the experimental gas phase geometries are only available for all hypohalous acids and perchloric acid. For the rest of the HXOn compounds, the comparison has been made with high-level ab initio calculations available in the literature. All of these geometrical data are gathered in Table 1. The inspection of the results revealed that our calculated geometries are in good to excellent agreement with both the experimental and theoretical ones from the literature. As far as we are concerned, high-level ab initio calculations are not available for HIO3, HBrO4, and HIO4. Therefore, this is the first time that such results are reported.
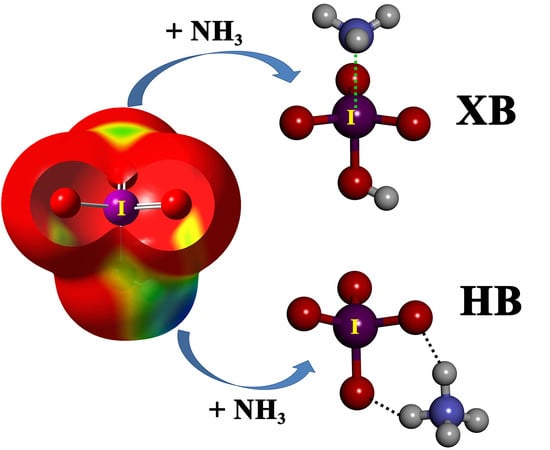
We have computed the molecular electrostatic potential (MEP) surfaces of the halogen oxoacids, paying special attention to the regions where the hydrogen and the halogen atoms are located, i.e., where the hydrogen and halogen bonding can be established (Figure 1). The MEP values associated with these regions are gathered in Table 2. A positive electrostatic potential region is located at the outermost region of both the H and halogen atoms in all cases, except for F in HFO, implying favorable formation of the complexes of HXOn with electron-rich systems, such as NH3 and Cl−. In this regard, the MEP values for the hydrogen bonding interaction are always larger than the corresponding MEP values for the halogen bonding for the same oxoacid, suggesting that, from the electrostatic point of view, the HB complex will be the preferred arrangement. For example, the difference between HB and XB MEP values oscillates between 6.2 and 47.9 kcal·mol−1 for HIO3 and HClO4, respectively. In the HB region, for the HXO and HXO2 series of compounds, the MEP values diminish on going from X = F to X = I. The opposite is observed for the HXO4 compounds, with MEP values increasing from X = Cl to X = I. However, for the HXO3 oxoacids, the MEP values increase from X = Cl to X = Br to then decrease for X = I. In the XB region, the MEP values increase on going from X = Cl to X = I, as expected. For each X, the HB and XB MEP values follow different trends: the former values are very similar, except for HXO4, which is sensibly larger, whereas the latter values increase from X = Cl to X = Br and decrease for X = I. In addition, we have compared the XB MEP values with the X–OH distances and found a good linear correlation (R2 = 0.900, Figure S1 of the Supplementary Materials). However, no linear correlation is observed when comparing the O–H distances with the HB MEP values (R2 = 0.248, Figure S2 of the Supplementary Materials). Thus the XB MEP results are able to reproduce the geometric results for the oxoacids, as opposed to the HB MEP results.

2.2. Geometrical Features and Energetics

We have considered two types of complexes between the halogen oxoacids and the Lewis bases, namely hydrogen-bonded (HB) complexes, formed through the interaction between either N atom (from ammonia) or Cl− and the hydrogen atom of the oxoacid, and halogen-bonded (XB) complexes, formed through the interaction between N or Cl− and the halogen atom of the oxoacid. At the RI-MP2/aug-cc-pVTZ level, both HB and XB complexes are local minima for all oxoacids, except for the fluorine derivative, for which the HB complex is the only one obtained, as expected from the abovementioned MEP results. In Table 3 and Table 4 we have put together the interaction energies and equilibrium distances for the NH3 and Cl− complexes, respectively. The structure of the complexes is essentially independent of the nature of the halogen atom. For example, the geometry of all HB and XB HBrOn complexes is reported in Figure 2 and Figure 3, respectively.
Let us first analyze the NH3 HB complexes. From the inspection of the results (Table 3), we observe that the N···H equilibrium distances range between 1.776 and 1.057 Å for HIO and HBrO4 complexes, respectively. These distances are much shorter than the sum of the van der Waals radii of N and H atoms (2.86 Å) [70]. These results indicate that the interaction established in these HB complexes is strong, as reflected in their interaction energies (ΔE) that range between −10.7 and −20.8 kcal·mol−1 for HBrO and HIO4 complexes, respectively. For comparison purposes, the interaction energy of the H3N···H2O complex, computed at the MP2/aug-cc-pVTZ level, is −6.70 kcal·mol−1 [32], much smaller than our reported values. In fact, for some of them (HXO4), a proton transfer is observed; the largest ΔE values were observed for the HClO4, HBrO4, and HIO4 complexes with NH3 (−17.7, −20.1, and −20.8 kcal·mol−1, respectively), which have quite short interatomic N···H distances (1.126, 1.057, and 1.061 Å, respectively) accompanied by the expected lengthening of the H–O distance by 0.429, 0.680, and 0.675 Å, respectively. The smallest ΔE values and the largest intermolecular HB distances were obtained for the HXO:NH3 complexes, and are constant for every halogen atom (ca. −11 kcal·mol−1 and ca. 1.77 Å, respectively). Nearly constant ΔE values were also observed for the HXO2 complexes, though a little bit larger than for the HXO ones. In fact, the N···H distances are the same for both HXO and HXO2 complexes. Particularly, the HXO2 complexes show an additional intermolecular interaction, an HB between the X=O oxygen atom, and an NH3 hydrogen atom, with increasing O···H distances (2.148, 2.191, and 2.259 Å for X = Cl, Br, and I, respectively) due to the concomitant lengthening of the X=O distance. Significant variations appear for the HXO3:NH3 complexes, yielding larger ΔE values and shorter intermolecular HB distances than those for the HXO and HXO2 complexes. Thus, the interaction energy increases, the N···H distances shorten, and the O–H distances lengthen with the number of oxygen atoms because of the increasing electron-withdrawing character of the XOn moiety, making the H atom much more acidic. Moreover, for n = 3 and n = 4, the ΔE values of the HXOn complexes are not constant, unlike for n = 1 and n = 2, obtaining the largest values for X = I, most likely due to the increasing impact that the oxygen atoms have on the highly polarizable iodine atom.
The results for the chloride HB complexes (Table 4) follow the same trends that have just been mentioned for the NH3 HB complexes. Thus, a good linear correlation (R2 = 0.888, Figure S3 of the Supplementary Materials) is found when comparing ΔE values of NH3 and Cl− HB complexes. Notwithstanding, this correlation is improved (R2 = 0.960) when an outlier is removed (HIO3). In this regard, ΔE values for HXO, on one hand, and for HXO2:Cl− complexes, on the other hand, are constant. In addition, the Cl···H equilibrium distances range between 1.918 and 1.333 Å for HFO and HBrO4 complexes, respectively, larger than the ones corresponding to the HB NH3 complexes, because of the larger size of the Cl atom. Again, these distances are much shorter than the sum of the van der Waals radii of Cl and H atoms (3.02 Å) [70]. The interaction is much stronger (ΔE = −24.0 to −49.1 kcal·mol−1 for HBrO and HIO4 complexes, respectively) than that found for the HB NH3 complexes because of the anionic nature of the chloride. Now, proton transfer is not only observed for HXO4 but for HXO3 complexes as well. The interaction energy increases, the HB distances shorten (Cl···H distances from 1.333 to 1.491 Å) to values quite close to the RI-MP2/aug-cc-pVTZ computed distance in hydrogen chloride (1.275 Å), and the O–H distances lengthen (within 0.292–0.633 Å range) with the number of oxygen atoms as found in the HB NH3 complexes.
Now, let us analyze the XB complexes, starting with the NH3 ones. From the inspection of the results, gathered in Table 3, we observe that the N···X equilibrium distances range from 3.240 to 2.340 Å for HClO4 and HIO4 complexes, respectively, which, at the same time, are the ones with the smallest and largest ΔE values (−2.2 and −20.2 kcal·mol−1, respectively). All of these distances are much shorter than the sum of the van der Waals radii of either Cl, Br, or I and N atoms (3.48, 3.52, and 3.70 Å, respectively) [70]. These results indicate that the interaction in these XB complexes is attractive, as can be interpreted from their negative ΔE values. Despite the size of the halogen atom increases on going from Cl to I, the shortest and largest XB equilibrium distances were observed for the HIOn and HClOn complexes, with the HBrOn complexes being intermediate between both. Another intimately related general trend was observed in the binding energies of all these complexes: their value decreases as the size of the halogen increases, a fact that can be related to the deeper σ-hole observed for the iodine derivatives (Figure 1), as predicted by our MEP calculations, which results in quite short N···I distances. Thus, in each series of the HXOn complexes, the most and least stable complexes correspond to the iodine and chlorine derivatives, respectively, with the bromine complexes being intermediate between both. For example, in the HXO2:NH3 series, the ΔE values are −4.4, −6.9, and −12.5 kcal·mol−1, with N···X distances of 2.888, 2.755, and 2.649 Å for X = Cl, Br, and I, respectively. On the other hand, in each series of complexes for a given n, the interaction energy increases from n = 1 to n = 3, i.e., as the number of oxygen atoms augments. For instance, in the HClOn:NH3 series, the ΔE values are −4.3, −4.4, and −4.8 kcal·mol−1 for n = 1, 2, and 3, respectively. However, for n = 4, the interaction energy drops to −2.2 kcal·mol−1. The same trend is also observed for the HBrOn:NH3 series. Unlike HClOn and HBrOn, the ΔE values of the iodine oxoacids increase all the way from n = 1 to n = 4. These results can be explained in terms of the accessibility of the halogen atom by the Lewis base. In free HClO4 and HBrO4, the O–X–OH bond angles are 103.7° and 102.7°, and the X=O bond lengths are 1.42 and 1.58 Å, whereas in HIO4 that bond angle is a little bit smaller (101.5°) and, most importantly, the I=O bond length is much longer (1.76 Å), moving the three oxo oxygen atoms a little bit further away, resulting in less repulsion with the electron-rich N atom of NH3 when approaching the HIO4 molecule. To some extent, these interaction energy results are in agreement with the MEP results (the largest ΔE values are obtained for the molecules with the largest HB MEP values, Table 2), meaning that electrostatics plays an important role in the stabilization of the complexes.
Just as in the HB complexes, the results for the chloride XB complexes (Table 4) follow the same trends as the NH3 XB complexes, with interaction energies that are substantially more negative with Cl− than NH3. As a matter of fact, the comparison of ΔE values of NH3 and Cl− XB complexes yields a good linear correlation (R2 = 0.953, Figure S4 of the Supplementary Materials). Therefore, in each series of the complexes, the most and least stable complexes in the HXOn series correspond to the iodine and chlorine derivatives, respectively. In addition, in each series of complexes for a given n, the interaction energy increases from n = 1 to n = 3, and then drops for n = 4, except for HIOn for which the ΔE values increase from n = 1 to n = 4. The Cl···X equilibrium distances range between 3.313 and 2.476 Å for HClO4 and HBrO4 complexes, respectively. As expected from the large and negative ΔE values, these distances are much shorter than the sum of the van der Waals radii of either Cl, Br, or I and Cl atoms (3.64, 3.68, and 3.86 Å, respectively) [70].
Comparison of the energetics of the complexes indicates that the only XB complexes that are more favored than the HB ones are HIO:NH3, HIO:Cl−, HIO2:Cl−, and HXO3:Cl−. Therefore, as the number of the O atoms increases, the XB complexes with an anionic Lewis base are being more favored than the HB ones, especially those with X = I (the halogen atom with the deepest σ-hole), except for those formed with HXO4 due to the accessibility of the X atom by the Lewis base.

2.3. Electron Density Analysis

The AIM methodology was applied to evaluate the properties of the charge density for our systems. The topological analysis of the electron density reveals the presence of a single intermolecular bond critical point (BCP) that connects the interacting atom of the Lewis base (N or Cl) with either the H or X atom of HXOn in HB and XB complexes, connected through the corresponding bond paths. For example, the molecular graphs of all HClOn:NH3 complexes are shown in Figure 4. Moreover, for HXO2:NH3 and HXO4:NH3 HB complexes, an additional BCP is located between an H atom of NH3 and an O atom of the oxoacid, giving rise to the formation of a ring critical point. At the intermolecular BCPs, the values of the electron densities, ρ, range between 0.299 and 0.047 a.u. for HXOn:NH3 HB complexes, between 0.218 and 0.050 a.u. for HXOn:Cl− HB complexes, between 0.076 and 0.008 a.u. for HXOn:NH3 XB complexes, and between 0.084 and 0.011 a.u. for HXOn:Cl− XB complexes (Table 5 and Table 6). Moreover, very large and negative values of the Laplacian, ∇2ρ, are obtained for the HB complexes where proton abstraction occurs (Table 5), namely all HXO4 HB complexes and HXO3:Cl− HB ones, consistent with the existence of a covalent bond. For the rest of the HB complexes, HXOn:Cl− XB complexes (except that with HClO4), HIOn:NH3 complexes, and the HBrO:NH3 complex, positive ∇2ρ values are accompanied by negative values of the total electron density energy, (Table 5), which indicate a partial covalent nature of these interactions [71,72]. For the rest of the XB complexes, the positive values accompanying ∇2ρ and H, in addition to the low ρ values, are genuine descriptors of charge-depleted intermolecular regions at BCPs, expected of closed-shell interactions [73,74,75,76,77,78,79,80,81].
The graphical representations of the electron density at the intermolecular BCP versus the intermolecular equilibrium distance (Figure 5) have good second-order polynomial trendlines, with correlation coefficients R2 = 0.950 for all HB complexes, and 0.946 and 0.823 for NH3 and Cl− XB complexes, respectively. There is also an excellent second-order polynomial fitting for the representation of ρ at the intermolecular BCP in HB complexes, ρHB, versus the O–H distance (R2 = 0.999 and 1.0 for NH3 and Cl− complexes, respectively, Figure S5 of the Supplementary Materials).
A comparison of the binding energies with the properties of the intermolecular BCPs reveals an interesting trend: the higher the electron density at the BCP, the stronger the interaction. The same trend applies to the Laplacian. In fact, there is a very good polynomial correlation (Figures S6 and S7 of the Supplementary Materials) between the interaction energies and the values of either ∇2ρHB (R2 = 0.837–0.975) or ρXB (R2 = 0.824–0.995). These results point out that the ρXB and ∇2ρHB values can be used as a measure of bond order for this type of interaction. This is in line with other studies, especially on hydrogen-bonded systems, where it was found that the ρ value is a good descriptor of the strength of the interaction [75,82].

2.4. Natural Bond Orbital Analysis

A Natural Bond Orbital (NBO) analysis was carried out to further analyze the geometrical, energetical, and topological characteristics of these HB and XB interactions between the halogen oxoacid derivatives and the Lewis bases. We have examined all possible intermolecular interactions between occupied (donor) Lewis-type NBOs and vacant (acceptor) non-Lewis NBOs and estimated their energetic importance by the second-order perturbation theory. According to the NBO analysis, the interaction is primarily based on a charge donation from the lone pairs of either the N atom of NH3 or chloride Cl to the vacant σ* antibonding orbital of the H–O bond in the HB complexes of HXOn [Lp(N) → σ*(H–O)], and to the vacant σ* antibonding orbital of the X–OH bond in the HXOn XB complexes, as derived from the calculated second-order orbital perturbation energies (E(2)) listed in Table 7. In the case of the HB complexes, very large E(2)HB values were obtained (between 56.8 and 29.2 kcal·mol−1 for the NH3 complexes and between 80.8 and 49.8 kcal·mol−1 for the Cl− ones) due to the proximity of the interacting groups. Significant E(2)XB values were also obtained for the XB complexes, with increasing values as we move from X = Cl to X = I. Thus, E(2)XB is maximum for HIOn complexes, the ones with the deepest σ-holes, and minimum for HClOn complexes, the ones with the shallowest σ-holes. In fact, in nine of the HB complexes (where a proton transfer was observed) and two of the XB complexes, the NBO method is not able to properly recognize the constituent molecules (Table 7) most likely due to the proximity of the interacting groups. Consequently, a significant charge is transferred from either the NH3 or Cl− unit to the oxoacid, even in the cases when no proton transfer complexes are considered (up to 0.105 e and 0.181 e in NH3 and Cl− HB complexes, and up to 0.179 e and 0.437 e in NH3 and Cl− XB complexes). In the case of the XB complexes, the E(2) values for the NH3 complexes (between 28.4 and 0.3 kcal·mol−1) are smaller than the corresponding ones for their HB counterparts. This is not the case for Cl− XB complexes, with E(2)XB values that are larger than their HB counterparts for HXO complexes.
The secondary intermolecular interaction found by means of the AIM analysis in HXO2:NH3 HB complexes is also found in the NBO analysis [Lp(O) → σ*(H–N)], though they contribute with very small E(2) values (0.7, 1.0, and 1.5 kcal·mol−1 for X = Cl, Br, and I, respectively) compared to the ones that were obtained for the primary HB interaction.
In addition, we have also compared the charge transfer with the second-order orbital perturbation energies, obtaining a very good linear correlation for NH3 and Cl− HB (R2 = 0.995 and 0.951, respectively, Figure S8 of the Supplementary Materials) and XB (R2 = 0.978 (excluding HIO4) and 0.955, respectively, Figure S9 of the Supplementary Materials) complexes. Therefore, the larger the E(2) energy, the larger the charge transfer, irrespective of the nature of the complexes.

2.5. Energy Partition Scheme

The physical nature of these HB and XB interactions has been analyzed by means of SAPT calculations. The energy contributions obtained from the SAPT partitioning scheme are listed in Table S1 (HB) and Table S2 (XB) of the Supplementary Materials and the corresponding terms are represented in Figure 6 (HB) and Figure 7 (XB). Some complexes have been removed from the analysis (proton transfer complexes and HClO3, HBrO4, and HIO4 XB complexes with Cl−) because they yield misleading results, most likely due to the proximity of the interacting units. The SAPT analysis revealed that the electrostatic term, Eel, is negative for all complexes, larger for anionic than for neutral complexes, with values ranging from −34.0 to −18.8 kcal·mol−1 and from −40.1 to −30.5 kcal·mol−1 for HXOn:NH3 and HXOn:Cl− HB complexes, respectively. The same behavior is observed for XB complexes, with Eel values between −76.4 and −4.2 kcal·mol−1 and between −77.3 and −9.4 kcal·mol−1 for HXOn:NH3 and HXOn:Cl− complexes, respectively.
Eel is the most important attractive contribution in all cases, with a relative weight within all attractive forces greater than 53.2% in HB complexes and greater than 47.3% in XB complexes. In addition, the electrostatic contribution becomes larger with the increasing number of O atoms in HB complexes. For instance, the Eel values are −19.9, −25.1, and −29.1 kcal·mol−1 for HClO:NH3, HClO2:NH3, and HClO3:NH3 HB complexes, respectively. In XB complexes, however, the Eel values increase on going from X = Cl to X = I, due to the smallest and largest σ-holes for these atoms, respectively, as observed in HXO:NH3 XB complexes (Eel = −11.9, −22.0, and −30.4 kcal·mol−1 for X = Cl, Br, and I, respectively). In general, the induction term, Ei, is the second most important attractive contribution. The Eel term, Ei, becomes larger with the number of oxygen atoms in HB complexes, as it usually increases with the size of the X atom in XB complexes. The smallest contribution, the dispersion energy, Ed, is kept more or less constant within each HXOn HB series and, at the same time, it becomes larger within each HXOn XB series, as expected from the high polarizability of the heavier X atoms.

3. Theoretical Methods

All of the geometries of the systems were fully optimized at the resolution of the identity second-order Møller–Plesset perturbation theory (RI-MP2) with the aug-cc-pVTZ basis set [83,84]. For iodine atoms [85], the aug-cc-pVTZ-PP pseudo potential basis set was used. Harmonic vibrational frequencies were computed at the same level used in order to verify that the structures obtained correspond to local minima.
The energies of the systems were refined by using the CCSD(T)/CBS method. The CCSD(T) technique provides reliable interaction energies only if they are combined with extended atomic orbital (AO) basis sets, and the larger the basis set, the better the interaction energies that result. Owing to the rather strong dependence of the interaction energy on the AO-basis-set size, it is recommended that the relevant calculations be performed at the complete basis-set (CBS) limit. Different extrapolation schemes have been introduced and the scheme of Helgaker et al. [86,87] has become most widely used. Here, the Hartree-Fock (HF) and correlation (MP2) energies are extrapolated separately as shown in Equations (1) and (2), respectively:
EX[HF] = ECBS[HF] + A e−αX
EX[MP2] = ECBS[MP2] + BX−3
ECBS[CCSD(T)] = ECBS[HF] + ECBS[MP2] + (E[CCSD(T)] − E[MP2])AVTZ
where EX and ECBS are the energies for the basis set with the largest angular momentum X and for the complete basis set, respectively. The CCSD(T)/CBS level can be attained via a separate extrapolation of the MP2 and higher-order correlation energies towards the basis-set limit (Equation (3)). Here, each of the components is differently sensitive to the AO basis set: the MP2 correlation energy is the more slowly converging, and the larger the basis set used in the extrapolation, the better. In our case, we have used a two-point extrapolation scheme by using the aug-cc-pVTZ and the aug-cc-pVQZ basis sets. The third term, called the CCSD(T) correction term (E[CCSD(T)] − E[MP2)], is determined as the difference between the CCSD(T) and MP2 energies and converges much faster than the MP2 correlation energy, the second term. The use of such a term is possible because the MP2 and CCSD(T) energies converge with basis-set size in a very similar way; consequently, its difference is much less basis-set-dependent and much smaller basis sets can be applied. In our case, we have used the aug-cc-pVTZ (AVTZ) basis set to compute the CCSD(T) correction. All of the geometry optimizations described herein were carried out by using TURBOMOLE version 7.0 [88] and CBS calculations were computed by using the MOLPRO program [89].
Binding energies were obtained as the difference between the energy of the complex and the energies of the optimized isolated monomers.
The bonding characteristics were analyzed by means of the Atoms-in-Molecules (AIM) theory [90,91]. For this purpose, we have located the most relevant bond critical points (BCP), and evaluated the electron density at each of them, with the facilities of AIMALL programs [92]. All of the interactions were characterized by the formation of a BCP between the atoms involved that are connected by the corresponding bond paths.
The Natural Bond Orbital (NBO) method [93] has been employed to evaluate atomic charges using the NBO-3.1 program, included within the Gaussian-09 program, and to analyze charge-transfer interactions between occupied and empty orbitals. Because MP2 orbitals are nonexistent, the charge-transfer interactions have been computed using the M06-2X functional with the aug-cc-pVTZ basis set at the MP2/aug-cc-pVTZ complex geometries, so that at least some electron correlation effects could be included.
The SAPT (Symmetry Adapted Perturbation Theory) [94] method allows for the decomposition of the interaction energy into different terms related to physically well-defined components, such as those arising from electrostatic, exchange, induction, and dispersion terms. The interaction energy can be expressed within the framework of the SAPT method as:
Eint = Eel(1) + Eexch(1) + Ei(2) + ED(2)
where Eel(1) is the electrostatic interaction energy of the monomers, each one with its unperturbed electron distribution; Eexch(1) is the first-order exchange energy term; Ei(2) denotes the second-order induction energy arising from the interaction of permanent multipoles with induced multipole moments and charge-transfer contributions, plus the change in the repulsion energy induced by the deformation of the electronic clouds of the monomers; and ED(2) is the second-order dispersion energy, which is related to the instantaneous multipole-induced multipole moment interactions plus the second-order correction for coupling between the exchange repulsion and the dispersion interactions.
The density fitting DFT-SAPT (DF-DFT-SAPT) formulation has been used to investigate interaction energies. In this approach, the energies of interacting monomers are expressed in terms of orbital energies obtained from the Kohn–Sham density functional theory [95,96]. In addition to the terms listed in Equation (4), a Hartree–Fock correction term δ(HF), which takes into account higher-order induction and exchange corrections, has been included [97]. The DF-DFT-SAPT calculations have been performed using the PBE0/aug-cc-pVTZ/aug-cc-pVTZ-PP computational method [98]. As an auxiliary fitting basis set, the JK-fitting basis of Weigend [99] was employed. The cc-pVQZ JK-fitting basis was used for all atoms. For the intermolecular correlation terms, i.e., the dispersion and exchange-dispersion terms, the related aug-cc-pVTZ MP2-fitting basis of Weigend, Köhn, and Hättig [100] was employed. All SAPT calculations have been carried out with the MOLPRO program [89].

4. Conclusions

In the present manuscript, we have analyzed the formation of HB and XB complexes with two Lewis bases (NH3 and Cl−) and the halogen oxoacids, HXOn from a theoretical point of view. The geometry of the HB and XB complexes is very similar within each HXOn series and, therefore, it is independent of the X atom. The interaction is quite strong for both types of complexes, giving rise to large interaction energies and intermolecular equilibrium distances much shorter than the sum of the van der Waals radii of the atoms involved in the interaction. In fact, proton transfer was generally observed in complexes with three or four oxygen atoms, namely, HXO4:NH3, HClO3:Cl−, HBrO3:Cl−, and HXO4:Cl−. The interaction energies generally increase with the number of O atoms. Comparison of the energetics of the complexes indicates that the only XB complexes that are more favored than those of HB are HIO:NH3, HIO:Cl−, HIO2:Cl−, and HIO3:Cl−. The atoms-in-molecules analysis revealed the presence of a bond critical point between the atoms involved in the interaction. Moreover, good correlations were obtained between electron density and its Laplacian values with intermolecular equilibrium distances. The topological analysis indicates a partial covalent nature of the HB interactions, apart from the complexes where proton transfer was observed. The NBO calculations show the presence of large charge-transfer-stabilizing energies, E(2), in both HB and XB complexes, that usually increase as the number of O atoms increases. The SAPT calculations show that the most important energy contribution comes from electrostatics, followed by induction and dispersion. Both Eel and Ei values increase with the number of O atoms for HB complexes and with the size of the X atom for XB complexes.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/7/1/9/s1, Figure S1: Graphical representation of d(X–OH) (in Å) versus XB MEP (in kcal/mol) in halogen oxoacids, Figure S2: Graphical representation of d(O–H) (in Å) versus HB MEP (in kcal/mol) in halogen oxoacids, Figure S3: Graphical representation of interaction energies of HB HXOn:NH3 versus HB HXOn:Cl− (in kcal·mol−1), Figure S4: Graphical representation of interaction energies of XB HXOn:NH3 versus XB HXOn:Cl− (in kcal·mol−1), Figure S5: Second-order polynomial relationship between the O–H distance (in Å) and the electron density for HB, ρHB, complexes, Figure S6: Second-order polynomial relationship between the interaction energy, ΔE, (in kcal·mol−1) and the Laplacian of the electron density for HB, ∇2ρHB, complexes, Figure S7: Second-order polynomial relationship between the interaction energy, ΔE, (in kcal·mol−1) and the electron density for HB, ρHB, complexes, Figure S8: Value of the charge of the Lewis base, in e, (NH3, up, Cl−, down) versus. E(2)HB, in kcal·mol−1, for all HB complexes with no proton transfer, Figure S9: Value of the charge of the Lewis base, in e, versus. E(2)XB, in kcal·mol−1, for all XB complexes. Table S1: SAPT electrostatic, exchange, dispersion, and induction energy contributions (Eel, Eex, Ed, and Ei, respectively) of HB complexes. Energies in kcal·mol−1, Table S2: SAPT electrostatic, exchange, dispersion, and induction energy contributions (Eel, Eex, Ed, and Ei, respectively) of XB complexes. Energies in kcal·mol−1.

Author Contributions

D.Q. conceived and designed the calculations; D.Q. and A.F. analyzed the data; and D.Q. wrote the paper.

Funding

We thank the MINECO/AEI (projects CTQ2014-57393-C2-1-P and CTQ2017-85821-R FEDER funds) for financial support.

Acknowledgments

We thank the CTI at the Universitat de les Illes Balears for computational facilities.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Scheiner, S. Noncovalent Forces; Springer: Berlin, Germany, 2015. [Google Scholar]
  2. Schneider, H.J. Binding Mechanisms in Supramolecular Complexes. Angew. Chem. Int. Ed. 2009, 48, 3924–3977. [Google Scholar] [CrossRef] [PubMed]
  3. Hunt, P.A.; Ashworth, C.R.; Matthews, R.P. Hydrogen bonding in ionic liquids. Chem. Soc. Rev. 2015, 44, 1257–1288. [Google Scholar] [CrossRef] [PubMed]
  4. Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
  5. Meot-Ner, M. The Ionic Hydrogen Bond. Chem. Rev. 2005, 105, 213–284. [Google Scholar] [CrossRef] [PubMed]
  6. Schreiner, P.R. Metal-free organocatalysis through explicit hydrogen bonding interactions. Chem. Soc. Rev. 2003, 32, 289–296. [Google Scholar] [CrossRef] [PubMed]
  7. Desiraju, G.R. The C−H···O Hydrogen Bond:  Structural Implications and Supramolecular Design. Acc. Chem. Res. 1996, 29, 441–449. [Google Scholar] [CrossRef] [PubMed]
  8. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
  9. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel Bonding Interactions. Chem. Rec. 2016, 16, 473–487. [Google Scholar] [CrossRef]
  10. Murray, J.S.; Lane, P.; Politzer, P. Expansion of the σ-hole concept. J. Mol. Model. 2009, 15, 723–729. [Google Scholar] [CrossRef]
  11. Scheiner, S. The Pnicogen Bond: Its Relation to Hydrogen, Halogen, and Other Noncovalent Bonds. Acc. Chem. Res. 2013, 46, 280–288. [Google Scholar] [CrossRef] [PubMed]
  12. Wang, W.; Ji, B.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef] [PubMed]
  13. Murray, J.S.; Lane, P.; Clark, T.; Politzer, P. σ-hole bonding: Molecules containing group VI atoms. J. Mol. Model. 2007, 13, 1033–1038. [Google Scholar] [CrossRef] [PubMed]
  14. Kolar, M.H.; Hobza, P. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Bauzá, A.; Frontera, A. Aerogen Bonding Interaction: A New Supramolecular Force? Angew. Chem. Int. Ed. 2015, 54, 7340–7343. [Google Scholar] [CrossRef] [PubMed]
  17. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
  18. Politzer, P.; Murray, J.S. Halogen Bonding: An Interim Discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef] [PubMed]
  19. Desiraju, G.; Ho, P.; Kloo, L.; Legon, A.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef] [Green Version]
  20. Auffinger, P.; Hays, F.A.; Westhof, E.; Ho, P.S. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. USA 2004, 101, 16789–16794. [Google Scholar] [CrossRef] [PubMed]
  21. Metrangolo, P.; Carcenac, Y.; Lahtinen, M.; Pilati, T.; Rissanen, K.; Vij, A.; Resnati, G. Nonporous Organic Solids Capable of Dynamically Resolving Mixtures of Diiodoperfluoroalkanes. Science 2009, 323, 1461–1464. [Google Scholar] [CrossRef]
  22. Aakeroy, C.B.; Wijethunga, T.K.; Benton, J.; Desper, J. Stabilizing volatile liquid chemicals using co-crystallization. Chem. Commun. 2015, 51, 2425–2428. [Google Scholar] [CrossRef] [PubMed]
  23. Lu, Y.; Shi, T.; Wang, Y.; Yang, H.; Yan, X.; Luo, X.; Jiang, H.; Zhu, W. Halogen Bonding—A Novel Interaction for Rational Drug Design? J. Med. Chem. 2009, 52, 2854–2862. [Google Scholar] [CrossRef] [PubMed]
  24. Sirimulla, S.; Bailey, J.B.; Vegesna, R.; Narayan, M. Halogen Interactions in Protein–Ligand Complexes: Implications of Halogen Bonding for Rational Drug Design. J. Chem. Inf. Model. 2013, 53, 2781–2791. [Google Scholar] [CrossRef] [PubMed]
  25. Lu, Y.; Wang, Y.; Zhu, W. Nonbonding interactions of organic halogens in biological systems: Implications for drug discovery and biomolecular design. Phys. Chem. Chem. Phys. 2010, 12, 4543–4551. [Google Scholar] [CrossRef] [PubMed]
  26. Bew, S.P.; Ashford, P.A.; Fairhurst, S.A.; Hughes, D.L.; Legentil, L.; Liddle, J.; Pesce, P.; Nigudkar, S.; Wilson, M.A. Organocatalytic Aziridine Synthesis Using F+ Salts. Org. Lett. 2009, 11, 4552–4555. [Google Scholar] [CrossRef] [PubMed]
  27. Walter, S.M.; Kniep, F.; Herdtweck, E.; Huber, S.M. Halogen-Bond-Induced Activation of a Carbon–Heteroatom Bond. Angew. Chem. Int. Ed. 2011, 50, 7187–7191. [Google Scholar] [CrossRef] [PubMed]
  28. Kniep, F.; Jungbauer, S.H.; Zhang, Q.; Walter, S.M.; Schindler, S.; Schnapperelle, I.; Herdtweck, E.; Huber, S.M. Organocatalysis by Neutral Multidentate Halogen-Bond Donors. Angew. Chem. Int. Ed. 2013, 52, 7028–7032. [Google Scholar] [CrossRef] [PubMed]
  29. Metrangolo, P.; Meyer, F.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen Bonding in Supramolecular Chemistry. Angew. Chem. Int. Ed. 2008, 47, 6114–6127. [Google Scholar] [CrossRef] [PubMed]
  30. Bolton, O.; Lee, K.; Kim, H.J.; Lin, K.Y.; Kim, J. Activating efficient phosphorescence from purely organic materials by crystal design. Nat. Chem. 2011, 3, 205–210. [Google Scholar] [CrossRef] [PubMed]
  31. Bertani, R.; Metrangolo, P.; Moiana, A.; Perez, E.; Pilati, T.; Resnati, G.; Rico-Lattes, I.; Sassi, A. Supramolecular Route to Fluorinated Coatings: Self-Assembly Between Poly(4-vinylpyridines) and Haloperfluorocarbons. Adv. Mater. 2002, 14, 1197–1201. [Google Scholar] [CrossRef]
  32. Alkorta, I.; Blanco, F.; Solimannejad, M.; Elguero, J. Competition of Hydrogen Bonds and Halogen Bonds in Complexes of Hypohalous Acids with Nitrogenated Bases. J. Phys. Chem. A 2008, 112, 10856–10863. [Google Scholar] [CrossRef] [PubMed]
  33. Blanco, F.; Alkorta, I.; Solimannejad, M.; Elguero, J. Theoretical Study of the 1:1 Complexes between Carbon Monoxide and Hypohalous Acids. J. Phys. Chem. A 2009, 113, 3237–3244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Li, Q.Z.; Xu, X.S.; Liu, T.; Jing, B.; Li, W.Z.; Cheng, J.B.; Gong, B.A.; Sun, J.Z. Competition between hydrogen bond and halogen bond in complexes of formaldehyde with hypohalous acids. Phys. Chem. Chem. Phys. 2010, 12, 6837–6843. [Google Scholar] [CrossRef] [PubMed]
  35. Li, Q.Z.; Jing, B.; Li, R.; Liu, Z.B.; Li, W.Z.; Luan, F.; Cheng, J.B.; Gong, B.A.; Sun, J.Z. Some measures for making halogen bonds stronger than hydrogen bonds in H2CS–HOX (X = F, Cl, and Br) complexes. Phys. Chem. Chem. Phys. 2011, 13, 2266–2271. [Google Scholar] [CrossRef]
  36. Zhao, Q.; Feng, D.C.; Sun, Y.M.; Hao, J.C.; Cai, Z.T. Theoretical investigations of the H···π and X (X = F, Cl, Br, I)···π complexes between hypohalous acids and benzene. J. Mol. Model. 2011, 17, 1935–1939. [Google Scholar] [CrossRef] [PubMed]
  37. Sanchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Weak interactions between hypohalous acids and dimethylchalcogens. Phys. Chem. Chem. Phys. 2012, 14, 9880–9889. [Google Scholar] [CrossRef] [PubMed]
  38. Li, Q.; Li, H.; Gong, J.; Li, W.; Cheng, J. Competitive interaction between halogen and hydrogen bonds in NH2Br–HOX (X = F, Cl, and Br) complex. Int. J. Quantum Chem. 2012, 112, 2429–2434. [Google Scholar] [CrossRef]
  39. An, X.; Zhuo, H.; Wang, Y.; Li, Q. Competition between hydrogen bonds and halogen bonds in complexes of formamidine and hypohalous acids. J. Mol. Model. 2013, 19, 4529–4535. [Google Scholar] [CrossRef] [PubMed]
  40. Zabardasti, A.; Kakanejadifard, A.; Goudarziafshar, H.; Salehnassaj, M.; Zohrehband, Z.; Jaberansari, F.; Solimannejad, M. Theoretical study of hydrogen and halogen bond interactions of methylphosphines with hypohalous acids. Comput. Theor. Chem. 2013, 1–7. [Google Scholar] [CrossRef]
  41. Li, Q.Z.; Zhu, H.J.; Zhuo, H.Y.; Yang, X.; Li, W.Z.; Cheng, J.B. Complexes between hypohalous acids and phosphine derivatives. Pnicogen bond versus halogen bond versus hydrogen bond. Spectrochim. Acta A 2014, 132, 271–277. [Google Scholar] [CrossRef]
  42. Zabardasti, A.; Tyula, Y.A.; Goudarziafshar, H. Theoretical investigation of molecular interactions between sulfur ylide and hypohalous acids (HOX, X = F, Cl, Br, and I). J. Sulfur Chem. 2016, 38, 119–133. [Google Scholar] [CrossRef]
  43. An, X.; Yang, X.; Xiao, B.; Cheng, J.; Li, Q. Comparison of hydrogen and halogen bonds between dimethyl sulfoxide and hypohalous acid: Competition and cooperativity. Mol. Phys. 2017, 115, 1614–1623. [Google Scholar] [CrossRef]
  44. Kaur, D.; Kaur, R.; Chopra, G. Comparison of hydrogen- and halogen-bonding interactions in the complexes of the substituted carbonyl compounds with hypohalous acids and monohaloamines. Struct. Chem. 2018, 29, 207–215. [Google Scholar] [CrossRef]
  45. Rozen, R.P.; Mishani, E.; Kol, M. A novel electrophilic methoxylation (with a little help from fluorine). J. Am. Chem. Soc. 1992, 114, 7643–7645. [Google Scholar] [CrossRef]
  46. Molina, M.J.; Tso, T.L.; Molina, L.T.; Wang, F.C. Antarctic stratospheric chemistry of chlorine nitrate, hydrogen chloride, and ice: Release of active chlorine. Science 1987, 238, 1253–1257. [Google Scholar] [CrossRef] [PubMed]
  47. Tolbert, M.A.; Rossi, M.J.; Malhotra, R.; Golden, D.M. Reaction of chlorine nitrate with hydrogen chloride and water at antarctic stratospheric temperatures. Science 1987, 238, 1258–1260. [Google Scholar] [CrossRef] [PubMed]
  48. Wayne, R.P.; Poulet, G.; Biggs, P.; Burrows, J.P.; Cox, R.A.; Crutzen, P.J.; Hayman, G.D.; Jenkin, M.E.; Le Bras, G.; Moortgat, G.K.; et al. Halogen oxides: Radicals, sources and reservoirs in the laboratory and in the atmosphere. Atmos. Environ. 1995, 29, 2677–2881. [Google Scholar] [CrossRef]
  49. Rowland, F.S.; Molina, M.J. Chlorofluoromethanes in the environment. Rev. Geophys. 1975, 13, 1–35. [Google Scholar] [CrossRef]
  50. McGrath, M.P.; Rowland, F.S. A Comparative Study of the Diatomic Halogen Oxides in Their Ground Electronic States. J. Phys. Chem. 1996, 100, 4815–4822. [Google Scholar] [CrossRef]
  51. Bogan, D.J.; Thorn, R.P.; Nesbitt, F.L.; Stief, L.J. Experimental 300 K measurement of the rate constant of the reaction OH + BrO → products. J. Phys. Chem. 1996, 100, 14383–14389. [Google Scholar] [CrossRef]
  52. Burrows, J.P.; Wallington, T.J.; Wayne, R.P. Kinetics of the reaction of OH with ClO. J. Chem. Soc. Faraday Trans. 2 1984, 80, 957–971. [Google Scholar] [CrossRef]
  53. Plane, J.M.C.; Joseph, D.M.; Allan, B.J.; Ashworth, S.H.; Francisco, J.S. An Experimental and Theoretical Study of the Reactions OIO + NO and OIO + OH. J. Phys. Chem. A 2006, 110, 93–100. [Google Scholar] [CrossRef] [PubMed]
  54. De Souza, G.L.C.; Brown, A. Probing ground and low-lying excited states for HIO2 isomers. J. Chem. Phys. 2014, 141, 234303. [Google Scholar] [CrossRef] [PubMed]
  55. Drougas, E.; Kosmas, A.M. Computational Studies of (HIO3) Isomers and the HO2 + IO Reaction Pathways. J. Phys. Chem. A 2005, 109, 3887–3892. [Google Scholar] [CrossRef] [PubMed]
  56. Mellouki, A.; Talukdar, R.K.; Howard, C.J. Kinetics of the reactions of HBr with O3 and HO2: The yield of HBr from HO2 + BrO. J. Geophys. Res. 1994, 99, 22949–22954. [Google Scholar] [CrossRef]
  57. Khanniche, S.; Louis, F.; Cantrel, L.; Černušák, I. Investigation of the Reaction Mechanism and Kinetics of Iodic Acid with OH Radical Using Quantum Chemistry. ACS Earth Space Chem. 2017, 1, 227–235. [Google Scholar] [CrossRef]
  58. Andersen, H.V.; Hovmand, M.F. Review of dry deposition measurements of ammonia and nitric acid to forest. Ecol. Manag. 1999, 114, 5–18. [Google Scholar] [CrossRef]
  59. Fowler, D.; Coyle, M.; Skiba, U.; Sutton, M.A.; Cape, J.N.; Reis, S.; Sheppard, L.J.; Jenkins, A.; Grizzetti, B.; Galloway, J.N.; et al. The global nitrogen cycle in the twenty-first century. Philos. Trans. R. Soc. B 2013, 368, 1621–1622. [Google Scholar] [CrossRef]
  60. Behera, S.N.; Sharma, M.; Aneja, V.P.; Balasubramanian, R. Ammonia in the atmosphere: A review on emission sources, atmospheric chemistry and deposition on terrestrial bodies. Environ. Sci. Pollut. Res. 2013, 20, 8092–8131. [Google Scholar] [CrossRef] [PubMed]
  61. Fiore, A.M.; Naik, V.; Leibensperger, E.M. Air Quality and Climate Connections. J. Air Waste Manag. Assoc. 2015, 65, 645–685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  62. Halonen, L. Equilibrium structure and anharmonic force field of hypofluorous acid (HOF). J. Chem. Phys. 1988, 89, 4885–4888. [Google Scholar] [CrossRef]
  63. Deeley, C.M. Vibration-rotation spectra of deuterated hypochlorous acid and the determination of the equilibrium structure. J. Mol. Spectrosc. 1987, 122, 481–489. [Google Scholar] [CrossRef]
  64. Cohen, E.A.; Mcrae, G.A.; Tan, T.L.; Friedl, R.R.; Johns, J.W.C.; Noel, M. The ν1 Band of HOBr. J. Mol. Spectrosc. 1995, 173, 55–61. [Google Scholar] [CrossRef]
  65. Klaassen, J.J.; Lindner, J.; Leone, S.R. Observation of the ν1 OH(OD) stretch of HOI and DOI by Fourier transform infrared emission spectroscopy. J. Chem. Phys. 1996, 104, 7403–7411. [Google Scholar] [CrossRef]
  66. Casper, B.; Mack, H.-G.; Mueller, H.S.P.; Willner, H.; Oberhammer, H. Molecular Structures of Perchloric Acid and Halogen Perchlorates ClOClO3 and FOClO3. J. Phys. Chem. 1994, 98, 8339–8342. [Google Scholar] [CrossRef]
  67. Karton, A.; Parthiban, S.; Martin, J.M.L. Post-CCSD(T) ab Initio Thermochemistry of Halogen Oxides and Related Hydrides XOX, XOOX, HOX, XOn, and HXOn (X = F, Cl), and Evaluation of DFT Methods for These Systems. J. Phys. Chem. A 2009, 113, 4802–4816. [Google Scholar] [CrossRef] [PubMed]
  68. De Souza, G.L.C.; Brown, A. The ground and excited states of HBrO2 [HOOBr, HOBrO, and HBr(O)O] and HBrO3 (HOOOBr and HOOBrO) isomers. Theor. Chem. Acc. 2016, 135, 178–190. [Google Scholar] [CrossRef]
  69. Guha, S.; Francisco, J.S. A Theoretical Examination of the Isomerization Pathways for HBrO3 Isomers. J. Phys. Chem. A 2000, 104, 9321–9327. [Google Scholar] [CrossRef]
  70. Alvarez, S. A cartography of the van der Waals territories. Daltontrans 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [PubMed]
  71. Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
  72. Rozas, I.; Alkorta, I.; Elguero, J. Behavior of Ylides Containing N, O, and C Atoms as Hydrogen Bond Acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
  73. Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Significant evidence of C···O and C···C long-range contacts in several heterodimeric complexes of CO with CH3–X, should one refer to them as carbon and dicarbon bonds! Phys. Chem. Chem. Phys. 2014, 16, 17238–17252. [Google Scholar] [CrossRef] [PubMed]
  74. Espinosa, E.; Souhassou, M.; Lachekar, H.; Lecomte, C. Topological analysis of the electron density in hydrogen bonds. Acta Cryst. Sect. B Struct. Sci. 1999, 55, 563–572. [Google Scholar] [CrossRef] [Green Version]
  75. Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H···F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
  76. Matta, C.F.; Hernández-Trujillo, J. Bonding in Polycyclic Aromatic Hydrocarbons in Terms of the Electron Density and of Electron Delocalization. J. Phys. Chem. A 2003, 107, 7496–7504. [Google Scholar] [CrossRef]
  77. Vener, M.V.; Manaev, A.V.; Egorova, A.N.; Tsirelson, V.G. QTAIM Study of Strong H-Bonds with the O−H···A Fragment (A = O, N) in Three-Dimensional Periodical Crystals. J. Phys. Chem. A 2007, 111, 1155–1162. [Google Scholar] [CrossRef] [PubMed]
  78. Varadwaj, P.R.; Marques, H.M. The physical chemistry of coordinated aqua-, ammine-, and mixed-ligand Co2+ complexes: DFT studies on the structure, energetics, and topological properties of the electron density. Phys. Chem. Chem. Phys. 2010, 12, 2126–2138. [Google Scholar] [CrossRef] [PubMed]
  79. Cukrowski, I.; Matta, C.F. Hydrogen–hydrogen bonding: A stabilizing interaction in strained chelating rings of metal complexes in aqueous phase. Chem. Phys. Lett. 2010, 499, 66–69. [Google Scholar] [CrossRef] [Green Version]
  80. Varadwaj, P.R.; Varadwaj, A.; Peslherbe, G.H. An electronic structure theory investigation of the physical chemistry of the intermolecular complexes of cyclopropenylidene with hydrogen halides. J. Comput. Chem. 2012, 33, 2073–2082. [Google Scholar] [CrossRef] [PubMed]
  81. Varadwaj, A.; Varadwaj, P.R. Can a Single Molecule of Water be Completely Isolated Within the Subnano-Space Inside the Fullerene C60 Cage? A Quantum Chemical Prospective. Chem. Eur. J. 2012, 18, 15345–15360. [Google Scholar] [CrossRef] [PubMed]
  82. Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
  83. Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  84. Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
  85. Peterson, K.A.; Shepler, B.C.; Figgen, D.; Stoll, H. On the Spectroscopic and Thermochemical Properties of ClO, BrO, IO, and Their Anions. J. Phys. Chem. A 2006, 110, 13877–13883. [Google Scholar] [CrossRef] [PubMed]
  86. Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Olsen, J. Basis-set convergence of the energy in molecular Hartree–Fock calculations. Chem. Phys. Lett. 1999, 302, 437–446. [Google Scholar] [CrossRef]
  87. Halkier, A.; Klopper, W.; Helgaker, T.; Jørgensen, P.; Taylor, P.R. Basis set convergence of the interaction energy of hydrogen-bonded complexes. J. Chem. Phys. 1999, 111, 9157–9167. [Google Scholar] [CrossRef]
  88. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007. Available online: http://www.turbomole.com (accessed on 30 December 2018).
  89. Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Schütz, M.; Celani, P.; Knizia, G.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO, version 2010.1, a Package of ab Initio Programs. Available online: www.molpro.net. (accessed on 30 December 2018).
  90. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
  91. Popelier, P.L.A. Atoms in Molecules. An Introduction; Prentice Hall: Harlow, UK, 2000. [Google Scholar]
  92. Keith, T.A. Version 15.09.27 edn, 2015, TK Gristmill Software. Available online: aim.tkgristmill.com. (accessed on 30 December 2018).
  93. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  94. Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
  95. Misquitta, A.J.; Podeszwa, R.; Jeziorski, B.; Szalewicz, K. Intermolecular potentials based on symmetry-adapted perturbation theory with dispersion energies from time-dependent density-functional calculations. J. Chem. Phys. 2005, 123, 214103. [Google Scholar] [CrossRef]
  96. Hesselmann, A.; Jansen, G. The helium dimer potential from a combined density functional theory and symmetry-adapted perturbation theory approach using an exact exchange–correlation potential. Phys. Chem. Chem. Phys. 2003, 5, 5010–5014. [Google Scholar] [CrossRef]
  97. Moszynski, R. Symmetry-adapted perturbation theory for the calculation of Hartree-Fock interaction energies. Mol. Phys. 1996, 88, 741–758. [Google Scholar] [CrossRef] [Green Version]
  98. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  99. Weigend, F. A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
  100. Weigend, F.; Köhn, A.; Hättig, C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175–3183. [Google Scholar] [CrossRef]
Inorganics 07 00009 g001 550
Figure 1. Molecular electrostatic potential (MEP) on the 0.001 a.u. electron density isosurface of the halogen oxoacids. Energy values in kcal·mol−1.
Figure 1. Molecular electrostatic potential (MEP) on the 0.001 a.u. electron density isosurface of the halogen oxoacids. Energy values in kcal·mol−1.
Inorganics 07 00009 g001
Inorganics 07 00009 g002 550
Figure 2. The optimized structures of the HB complexes between HBrOn and NH3, and between HBrOn and Cl−.
Figure 2. The optimized structures of the HB complexes between HBrOn and NH3, and between HBrOn and Cl−.
Inorganics 07 00009 g002
Inorganics 07 00009 g003 550
Figure 3. The optimized structures of the XB complexes between HBrOn and either NH3 or Cl−.
Figure 3. The optimized structures of the XB complexes between HBrOn and either NH3 or Cl−.
Inorganics 07 00009 g003
Inorganics 07 00009 g004 550
Figure 4. Molecular graphs of HB and XB complexes of HClOn:NH3. The bond and ring critical points are represented by green and red dots, respectively. Only bond paths are depicted.
Figure 4. Molecular graphs of HB and XB complexes of HClOn:NH3. The bond and ring critical points are represented by green and red dots, respectively. Only bond paths are depicted.
Inorganics 07 00009 g004
Inorganics 07 00009 g005a 550Inorganics 07 00009 g005b 550
Figure 5. The second-order polynomial relationship between the intermolecular distance (in Å) and the electron density for HB, ρHB, (up) and XB, ρXB, (down) complexes.
Figure 5. The second-order polynomial relationship between the intermolecular distance (in Å) and the electron density for HB, ρHB, (up) and XB, ρXB, (down) complexes.
Inorganics 07 00009 g005aInorganics 07 00009 g005b
Inorganics 07 00009 g006 550
Figure 6. Symmetry-adapted perturbation theory (SAPT) electrostatic, exchange, dispersion, and induction energy contributions (Eel, Eex, Ed, and Ei, respectively) of HB complexes. Energies in kcal·mol−1.
Figure 6. Symmetry-adapted perturbation theory (SAPT) electrostatic, exchange, dispersion, and induction energy contributions (Eel, Eex, Ed, and Ei, respectively) of HB complexes. Energies in kcal·mol−1.
Inorganics 07 00009 g006
Inorganics 07 00009 g007 550
Figure 7. SAPT electrostatic, exchange, dispersion, and induction energy contributions (Eel, Eex, Ed, and Ei, respectively) of XB complexes. Energies in kcal·mol−1.
Figure 7. SAPT electrostatic, exchange, dispersion, and induction energy contributions (Eel, Eex, Ed, and Ei, respectively) of XB complexes. Energies in kcal·mol−1.
Inorganics 07 00009 g007
Table
Table 1. RI-MP2/aug-cc-pVTZ (theor) and experimental (exptl) geometries of halogen oxoacids (in angstroms and degrees).
Table 1. RI-MP2/aug-cc-pVTZ (theor) and experimental (exptl) geometries of halogen oxoacids (in angstroms and degrees).
CompoundSymmetryData TypeO–HX–OHH–O–XO–X–O–H
HFOCstheor0.9701.42997.9-
exptl [62]0.9661.43597.5-
HClOCstheor0.9691.697102.5-
exptl [63]0.9641.689103.0-
HBrOCstheor0.9691.829103.0-
exptl [64]0.9641.828103.0-
HIOCstheor0.9691.991104.2-
exptl [65]0.9641.991105.4-
HClO2C1theor0.9731.715103.6-
theor a0.9671.694104.0-
HBrO2C1theor0.9721.836104.6-
theor b0.9701.848104.4-
HIO2C1theor0.9701.979106.4-
theor c0.9681.990106.6-
HClO3C1theor0.9751.746102.932.4, 150.9
theor a0.9701.689102.5118.3, −0.4
HBrO3C1theor0.9771.824103.122.9, −92.3
theor d0.9671.821102.923.0, −92.5
HIO3C1theor0.9751.949107.041.2, −70.6
exptl e----
HClO4Cstheor0.9741.667103.40.0
exptl [66]0.9801.641105.00.0
HBrO4Cstheor0.9761.777103.80.0
exptl e----
HIO4Cstheor0.9751.915106.20.0
exptl e----
a CCSD(T)/cc-pVQZ [67]. b CCSD(T)/aug-cc-PVTZ-PP [68]. c CCSD(T)/aug-cc-pVTZ-PP [54]. d QCISD/6-311G(2d,2p) [69]. e No experimental data or benchmark calculation available.
Table
Table 2. Molecular electrostatic potential values (ΔE in kcal·mol−1) and interatomic distances (Å) of the hydrogen bonding (HB) and halogen bonding (XB) complexes with NH3.
Table 2. Molecular electrostatic potential values (ΔE in kcal·mol−1) and interatomic distances (Å) of the hydrogen bonding (HB) and halogen bonding (XB) complexes with NH3.
MoleculeHB XB
X = FX = ClX = BrX = IX = ClX = BrX = I
HXO59.755.853.550.623.731.139.3
HXO2-57.756.454.728.136.043.7
HXO3-56.054.455.731.940.949.5
HXO4-68.470.371.120.528.842.4
Table
Table 3. The interaction energies (ΔE in kcal·mol−1) and interatomic distances (Å) of the hydrogen bonding (HB) and halogen bonding (XB) complexes with NH3.
Table 3. The interaction energies (ΔE in kcal·mol−1) and interatomic distances (Å) of the hydrogen bonding (HB) and halogen bonding (XB) complexes with NH3.
Complex HB XB
withΔEN···HΔ(H–O)ΔEN···XΔ(X–OH)
HFO−11.01.7730.026---
HClO−11.11.7550.029−4.32.6380.023
HClO2−13.61.7660.033−4.42.8880.005
HClO3−14.51.6310.060−4.82.846−0.003
HClO4−17.71.1260.429−2.23.2400.011
HBrO−10.71.7660.028−7.12.5620.035
HBrO2−13.41.7660.034−6.92.7550.006
HBrO3−15.31.6210.061−8.12.7400.007
HBrO4−20.11.0570.680−5.22.8520.012
HIO−11.11.7760.027−11.42.6130.035
HIO2−14.51.7660.036−12.52.6490.008
HIO3−17.01.6390.059−14.92.6180.004
HIO4−20.81.0610.675−20.22.3400.005
Table
Table 4. The interaction energies (ΔE in kcal·mol−1) and interatomic distances (Å) of the hydrogen bonding (HB) and halogen bonding (XB) complexes with Cl−.
Table 4. The interaction energies (ΔE in kcal·mol−1) and interatomic distances (Å) of the hydrogen bonding (HB) and halogen bonding (XB) complexes with Cl−.
Complex HB XB
withΔECl−···HΔ(H–O)ΔECl−···XΔ(X–OH)
HFO−24.11.9180.050---
HClO−24.41.8760.059−13.12.4500.176
HClO2−30.41.7970.080−11.82.5970.210
HClO3−31.51.3970.462−12.32.6850.215
HClO4−44.91.3360.626−2.53.3130.079
HBrO−24.01.8760.060−21.52.5340.159
HBrO2−30.01.8130.076−22.12.6150.144
HBrO3−30.91.4120.421−24.02.6360.141
HBrO4−48.11.3330.633−17.42.4760.098
HIO−24.51.8730.060−29.82.6650.132
HIO2−30.61.8360.071−33.12.6770.103
HIO3−30.41.4910.292−38.12.6530.086
HIO4−49.11.3410.594−45.72.4780.056
Table
Table 5. Electron density (ρHB), Laplacian (∇2ρHB), and electron density total energy (HHB) in a.u. for the intermolecular bond critical points for HB complexes.
Table 5. Electron density (ρHB), Laplacian (∇2ρHB), and electron density total energy (HHB) in a.u. for the intermolecular bond critical points for HB complexes.
Complex NH3 Cl−
withρHB∇2ρHBHHBρHB∇2ρHBHHB
HFO0.0470.071−0.0130.0500.050−0.016
HClO0.0490.069−0.0140.0550.042−0.020
HClO20.0520.069−0.0160.0670.022−0.030
HClO30.0660.051−0.0270.184−0.522−0.178
HClO40.243−1.235−0.3670.217−0.710−0.226
HBrO0.0480.070−0.0130.0550.043−0.020
HBrO20.0500.070−0.0150.0640.027−0.028
HBrO30.0680.049−0.0280.177−0.477−0.167
HBrO40.299−1.857−0.5150.218−0.714−0.228
HIO0.0470.071−0.0130.0560.042−0.021
HIO20.0480.071−0.0140.0610.034−0.025
HIO30.0650.053−0.0260.143−0.283−0.118
HIO40.296−1.814−0.5050.214−0.689−0.221
Table
Table 6. Electron density (ρXB), Laplacian (∇2ρXB), and total electron density energy (HXB) in a.u. for the intermolecular bond critical points for XB complexes.
Table 6. Electron density (ρXB), Laplacian (∇2ρXB), and total electron density energy (HXB) in a.u. for the intermolecular bond critical points for XB complexes.
Complex NH3 Cl−
withρXB∇2ρXBHXBρXB∇2ρXBHXB
HFO------
HClO0.0260.0900.0010.0610.104−0.013
HClO20.0160.0570.0020.0470.098−0.006
HClO30.0180.0620.0010.0410.089−0.005
HClO40.0080.0310.0010.0110.0350.001
HBrO0.0360.101−0.0030.0580.088−0.013
HBrO20.0250.0740.0000.0520.088−0.009
HBrO30.0270.0740.0000.0520.084−0.009
HBrO40.0220.0600.0000.0750.044−0.023
HIO0.0400.095−0.0050.0530.077−0.013
HIO20.0380.086−0.0040.0530.075−0.012
HIO30.0420.080−0.0060.0580.069−0.015
HIO40.0760.065−0.0290.0840.023−0.035
Table
Table 7. Second-order perturbation stabilization energies for the donor-acceptor Lp(N) → σ*(H–O), Lp(Cl) → σ*(H–O) (E(2)HB), Lp(N) → σ*(X–OH), and Lp(Cl) → σ*(X–OH) (E(2)XB) and charge (in e) of the Lewis base of the complexes using Natural Bond Orbital (NBO) analysis. Energies in kcal·mol−1.
Table 7. Second-order perturbation stabilization energies for the donor-acceptor Lp(N) → σ*(H–O), Lp(Cl) → σ*(H–O) (E(2)HB), Lp(N) → σ*(X–OH), and Lp(Cl) → σ*(X–OH) (E(2)XB) and charge (in e) of the Lewis base of the complexes using Natural Bond Orbital (NBO) analysis. Energies in kcal·mol−1.
Complex withHB XB
NH3 Cl− NH3 Cl−
E(2)HBChargeE(2)HBChargeE(2)XBChargeE(2)XBCharge
HFO30.90.05449.8−0.880----
HClO33.10.06058.4−0.85810.60.04769.3−0.669
HClO236.80.06780.8−0.8193.00.01242.2−0.762
HClO355.30.102a−0.4972.90.01136.1−0.812
HClO4a0.368a−0.4130.3−0.0021.1−0.991
HBrO31.30.05857.5−0.85621.40.08476.0−0.673
HBrO234.10.06175.1−0.8268.40.03652.5−0.735
HBrO356.80.105a−0.5127.40.03344.9−0.754
HBrO4a0.398a−0.4073.50.01849.0−0.600
HIO29.20.05556.6−0.85426.70.09767.1−0.707
HIO231.10.05666.6−0.83719.20.07655.4−0.734
HIO352.50.100a−0.59317.70.082a−0.729
HIO4a0.392a−0.41628.40.179a−0.563
a The NBO method is not able to properly divide the complex into its molecular constituents.

Share and Cite

MDPI and ACS Style

Quiñonero, D.; Frontera, A. Hydrogen Bond versus Halogen Bond in HXOn (X = F, Cl, Br, and I) Complexes with Lewis Bases. Inorganics 2019, 7, 9. https://doi.org/10.3390/inorganics7010009

AMA Style

Quiñonero D, Frontera A. Hydrogen Bond versus Halogen Bond in HXOn (X = F, Cl, Br, and I) Complexes with Lewis Bases. Inorganics. 2019; 7(1):9. https://doi.org/10.3390/inorganics7010009

Chicago/Turabian Style

Quiñonero, David, and Antonio Frontera. 2019. "Hydrogen Bond versus Halogen Bond in HXOn (X = F, Cl, Br, and I) Complexes with Lewis Bases" Inorganics 7, no. 1: 9. https://doi.org/10.3390/inorganics7010009

APA Style

Quiñonero, D., & Frontera, A. (2019). Hydrogen Bond versus Halogen Bond in HXOn (X = F, Cl, Br, and I) Complexes with Lewis Bases. Inorganics, 7(1), 9. https://doi.org/10.3390/inorganics7010009

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop